Введение в машинное обучение и искусственные нейронные сети

Глава1. Введение в машинное обучение

Что такое машинное обучение

Машинное обучение (machine learning, ML) – это раздел информатики, который занимается разработкой и анализом алгоритмов, позволяющих компьютерам меняться под воздействием внешних факторов (обучаться). Алгоритмы обучения (learning algorithms) делают предсказания или принимают решения не на основе строго статических программных команд, а на основе обучающей выборки (т.е. обучающих данных), с помощью которой происходит настройка параметров модели. Для процесса настройки (fitting) модели по выборке данных применяются различные разделы математики: математическая статистика, методы оптимизации, численные методы, теория вероятностей, линейная алгебра, математический анализ, дискретная математика, теория графов, различные техники работы с цифровыми данными и др. Результатом работы алгоритма обучения является функция, которая аппроксимирует (восстанавливает) неизвестную зависимость в обрабатываемых данных.

Машинное обучение является не только математической, но и прикладной, инженерной дисциплиной. Практически ни одно исследование в области машинного обучения не обходится без последующего тестирования на реальных данных для проверки практической работоспособности разрабатываемого метода.

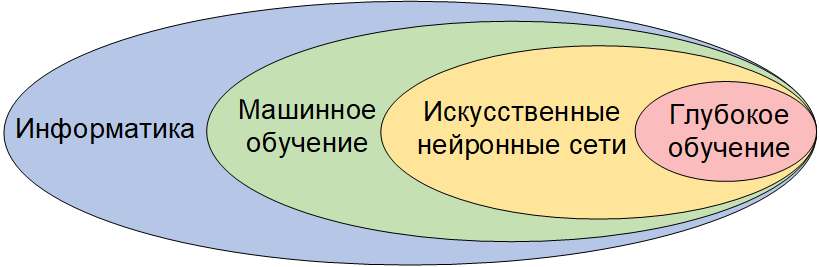
Когда говорят о машинном обучении, то часто имеют ввиду вновь ставшие популярными искусственные нейронные сети (ИНС) и глубокое обучение, которые являются моделями машинного обучения (рисунок 1.1), т.е. частными случаями методов распознавания образов, дискриминантного анализа, методов кластеризации и т. п.

Рис. 1.1 – Вложенность категорий

Типы обучения

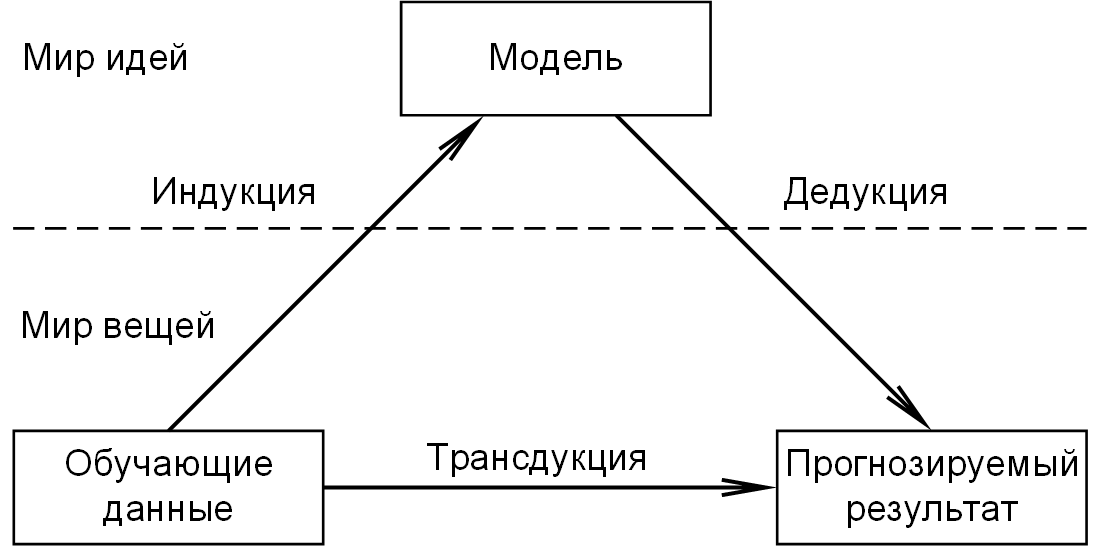
Есть три типа методов машинного обучения: дедуктивное, индуктивное и трансдуктивное.

Дедуктивное обучение или обучение «сверху-вниз», от общего к частному предполагает формализацию знаний экспертов и их перенос в компьютер в виде базы знаний. Дедуктивное обучение принято относить к области экспертных систем. Имеются знания, сформулированные экспертом и каким-либо образом формализованные через уравнения, теоремы, зависимости и т.д. Программа, экспертная система, выводит из этих правил конкретные факты и новые правила.

Индуктивное обучение или обучение «снизу-вверх», от частного к общему, обучение на примерах, обучение по прецедентам, основано на выявлении закономерностей в эмпирических данных, т.е. данных полученных путём наблюдения или эксперимента. Индуктивное обучение компьютеров принято относить к машинному обучению. Многие методы индуктивного обучения разрабатывались как альтернатива классическим статистическим подходам и тесно связаны с извлечением информации (information extraction) и интеллектуальным анализом данных (data mining). На основе эмпирических данных программа строит общее правило. Эмпирические данные могут быть получены самой программой в предыдущие сеансы её работы или просто предъявлены ей.

Трансдуктивное обучение [1.2] или обучение от частного к частному, позволяет на основе эмпирических данных без выявления общих закономерностей и формализации знаний сделать выводы о других эмпирических данных. Понятие трансдукции было предложено Владимиром Вапником в 1990 году: «При решении интересующей проблемы не решайте более общую проблему как промежуточный шаг. Постарайтесь получить ответ, который вам действительно нужен, но не более общий». Например, если не учитывать объекты без метки (рисунок 1.2), тогда невозможно правильно сегментировать множество, потому что слишком мало размеченных объектов.

Рис. 1.2 – Пример трансдуктивного обучения

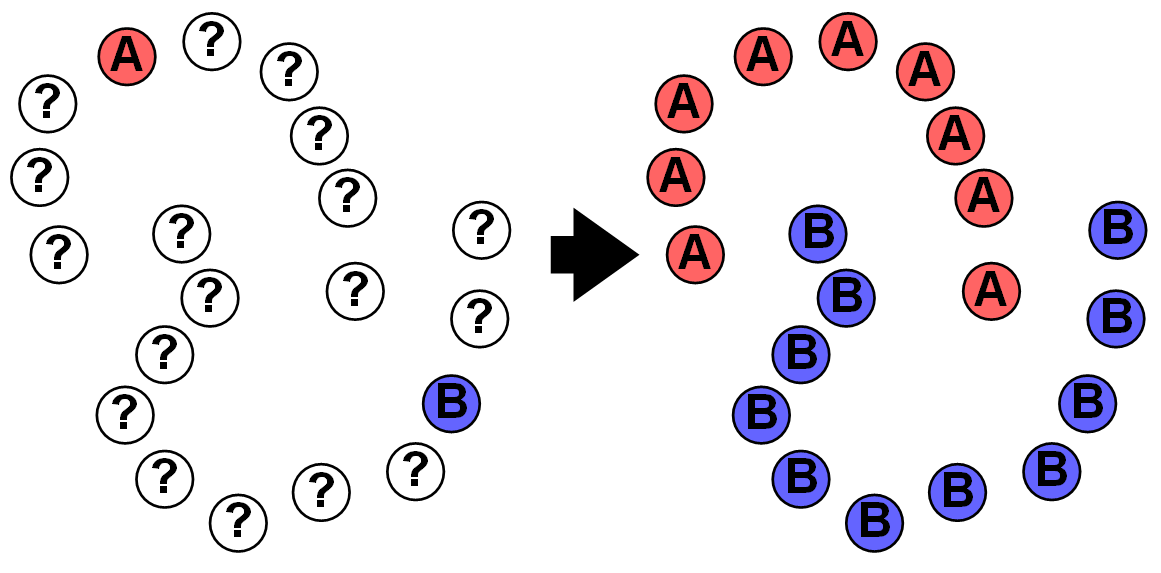
При решении задачи методом индукции, когда ищется общий ответ для всех возможных случаев, неразмеченные объекты не учитываются, их как бы нет для решающего задачу, потому что с точки зрения индуктивного обучения могут быть и другие неразмеченные объекты кроме имеющихся. Учёт присутствующих неразмеченных данных может кардинально изменить качество решения, но если появятся новые неразмеченные данные, то их появление может полностью изменить ответ. Трансдуктивное обучение применяется в некоторых методах машинного обучения с частичным привлечением учителя (semi-supervised learning). Взаимосвязь между тремя типами обучения можно увидеть на рисунке 1.3.

Рис. 1.3 – Три типа обучения

Будем считать задачу обучения экзаменом, размеченные объекты – как решённые учителем примеры, а неразмеченные объекты – как предоставленные учителем нерешённые примеры. С точки зрения дедуктивного обучения у вас уже есть формула, показанная вам учителем, с помощью которой вы можете решить все нерешённые задачи на экзамене, поэтому нет смысла решать предоставленные учителем нерешённые примеры. С точки зрения индуктивного обучения нерешённые примеры являются подобными тем, которые будут на экзамене. С точки зрения трансдуктивного обучения данные учителем нерешённые примеры и есть экзамен, т.е. эти же примеры будут на экзамене.

Способы обучения

Методы машинного обучения обычно разделяются на две обширные категории, в зависимости от наличия обучающего «сигнала» или «обратной связи» для алгоритма обучения: обучение с учителем (supervised learning) и обучение без учителя (unsupervised learning).

При обучении с учителем система обучается на примерах с заранее известными правильными ответами. На основе этих входных примеров и известных правильных ответов требуется восстановить зависимость между множеством примеров и множеством ответов, т.е. построить алгоритм, который будет выдавать достаточно точный ответ для любого примера. Совокупность примеров (входных объектов) и соответствующих им правильных ответов называется обучающей выборкой. Пусть обучающая выборка описывается парой значений 〈x, y〉, где x=〈x₁,x₂,…,x_n〉 – это данные (многомерный вектор признаков), y – это целевое значение (метка или правильный ответ). Надо найти функцию ƒ(x)=y.

Обучение без учителя, самообучение, происходит на примерах без заранее известных правильных ответов. Система сама находит внутренние взаимосвязи, зависимости, закономерности, существующие между объектами без вмешательства внешнего учителя, экспериментатора, человека. Пусть каждый объект описан вектором признаков x=〈x₁,x₂,…,x_n〉. Надо найти механизм, который описывает структуру этих данных, которая заранее не известна.

Комбинированные виды обучения применяют различные сочетания обоих типов обучения в одной программе. Например, обучение с частичным привлечением учителя, обучение с подкреплением и некоторые другие.

При обучении с подкреплением учителем является сама окружающая среда, модель среды или неявный учитель, например, одновременная активность нескольких нейронов в искусственной нейронной сети.

Не всегда удаётся найти хорошую обучающую выборку. Часто данные размечены не полностью, т.е. не для всех данных есть правильный ответ (метка). Разметка данных для машинного обучения является однообразным и долгим трудом. Обычно имеется небольшое количество размеченных данных и большое количество неразмеченных данных. В этом случае применяется обучение с частичным привлечением учителя. Его ещё называют полуавтоматическим обучением (semi-supervised learning). Многие исследователи машинного обучения обнаружили, что неразмеченные данные, при использовании в сочетании с небольшим количеством размеченных данных, могут значительно улучшить точность обучения. Обучение с частичным привлечением учителя является частным случаем трансдуктивного обучения.

Решаемые задачи

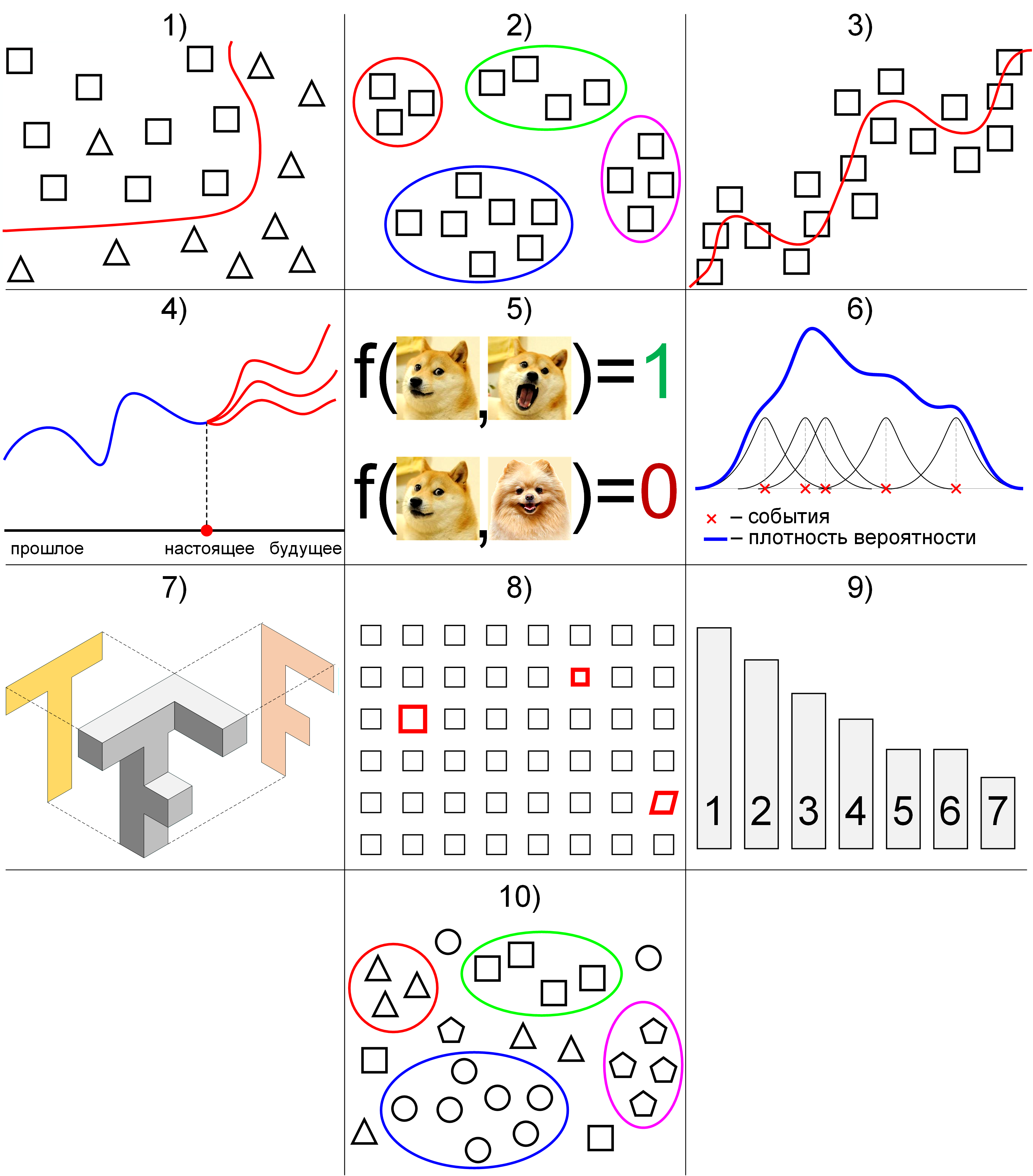
Методы машинного обучения разделяются по типам решаемых задач: классификация, кластеризация, регрессия, прогнозирование, идентификация, восстановление плотности распределения вероятности по набору данных, понижение размерности, одноклассовая классификация и выявление новизны, построение ранговых зависимостей и т.д. Продолжают возникать новые типы задач и даже целые новые дисциплины машинного обучения, например, добыча данных (data mining).

Классификация – разделение множества объектов или ситуаций на классы с помощью обучения с учителем. Классифицировать объект – значит, указать номер, имя или метку класса, к которому относится данный объект. Иногда требуется указать вероятность отношения объекта к классу. Например, по обучающей выборке фотографий котов и собак научиться различать изображения котов и собак.

Кластеризация (сегментация) – разделение множества объектов или ситуаций на кластеры с помощью обучения без учителя. Кластеризация (обучение без учителя) отличается от классификации (обучения с учителем) тем, что перечень групп четко не задан и определяется в процессе работы алгоритма, т.е. нет заранее определённых «правильных» ответов. Иногда указывается общее количество кластеров, но часто алгоритм сам выбирает оптимальное количество кластеров. Похожесть или близость объектов в кластере определяется через расстояние в многомерном пространстве признаков. Для этого нужно определить само пространство признаков (какие свойства измеряются) и метрику близости (как считается расстояние). Результаты кластеризации применяются при нахождении новых, ранее неизвестных знаний и зависимостей в данных (добыча данных или data mining). Например, задача нахождения целевой аудитории определённого товара путём анализа потребительских корзин покупателей с учётом пола, возраста, социального статуса, семейного положения и т.д.

Регрессия – нахождение зависимости выходной переменной от одной или нескольких независимых входных переменных с помощью обучения с учителем. В отличие он задач классификации, которые разделяют объекты на дискретное количество классов, задачи регрессии находят зависимости между непрерывными величинами. Например, нахождение зависимости между количеством съеденной пищи и весом тела.

Прогнозирование – это предсказание во времени. Прогнозирование похоже либо на регрессию, либо на классификацию в зависимости от данных задачи (непрерывные или дискретные данные), но в отличие от регрессии и классификации всегда направлено в будущее. В прогнозировании данные упорядочиваются по времени, которое является явным и ключевым параметром, а найденная зависимость экстраполируется в будущее. В прогнозировании применяются модели временных рядов.

Идентификация. Идентификация и классификация многими ошибочно понимаются как синонимы. Задача идентификации исторически возникла из задачи классификации, когда вместо определения класса объекта потребовалось уметь определять, обладает объект требуемым свойством или нет. Особенностью задачи идентификации является то, что все объекты принадлежат одному классу, и не существует возможности разделить класс на подклассы, т.е. сделать состоятельную выборку из класса, которая не будет обладать требуемым свойством. Если требуется определить человека по фотографии его лица, причём множество запомненных в базе людей постоянно меняется и появляются люди, которых не было в обучающем множестве, то это задача идентификации, которая не сводится к задаче классификации. В случае определения объекта по фотографии функция идентификации ƒ(x₁,x₂) принимает в качестве аргументов два вектора признаков фотографий, а на выходе равна либо 1 в случае фотографий одного и того же объекта либо 0 в случае фотографий разных объектов одного и того же класса.

Восстановление плотности распределения вероятности по набору данных (kernel density estimate). Данная задача является центральной проблемой математической статистики. Математическая статистика решает обратные задачи: по результату эксперимента определяет свойства закона распределения. Исчерпывающей характеристикой закона распределения является плотность распределения вероятностей. Например, известен возраст людей, берущих кредит в банке, требуется найти плотность распределения вероятности возрастов заёмщиков.

Понижение размерности данных и их визуализация. Является частным случаем кластеризации. Каждый объект может быть представлен в виде многомерного вектора признаков 〈x₁,x₂,…,x_n〉, нужно получить более компактное признаковое описание объекта 〈x₁,x₂,…,x_k〉, где k < n. Понижение размерности может помочь другим методам путём устранения избыточных данных. Используется при разведочном анализе и для устранения «проклятия размерности», когда данные быстро становятся разреженными при увеличении размерности пространства признаков. Например, дан список документов на человеческом языке, требуется найти документы с похожими темами.

Одноклассовая классификация и выявление новизны. Или задача поиска аномалий, выбросов, которые не относятся ни к одному кластеру. Нахождение объектов, которые отличаются по своим свойствам от объектов обучающей выборки. Является задачей обучения без учителя. Например, обнаружение инородных предметов (кости, камни, кусочки упаковки) в продуктах питания при их сканировании рентгеновским сканером при неразрушающем контроле качества продукции, обнаружение подозрительных банковских операций, обнаружение хакерской атаки, медицинская диагностика и т.д.

Построение ранговых зависимостей. Ранжирование – это процедура упорядочения объектов по степени выраженности какого-либо качества в порядке убывания этого качества. Задачами ранжирования являются: сортировка веб-страниц согласно заданному поисковому запросу, персонализация новостной ленты, рекомендации товаров (видео, музыки), адресная реклама.

Добыча данных (data mining) или интеллектуальный анализ данных [1.3] – совокупность методов обнаружения в данных ранее неизвестных, нетривиальных, практически полезных и доступных интерпретации знаний, необходимых для принятия решений в различных сферах человеческой деятельности. В данный момент добыча данных отделяется от машинного обучения в отдельную дисциплину. Интеллектуальный анализ данных и машинное обучение имеют различные цели: машинное обучение прогнозирует на основе известных свойств, полученных от обучающей выборки, а интеллектуальный анализ данных фокусируется на добыче новых ранее неизвестных зависимостей в данных. Однако обе дисциплины используют одинаковые методы.

Различные типы задач схематически представлены на рисунке 1.4.

Рис. 1.4 – Схематическое представление типов задач:
1) классификация; 2) кластеризация; 3) регрессия; 4) прогнозирование; 5) идентификация;
6) восстановление плотности распределения вероятности по набору данных;
7) понижение размерности; 8) одноклассовая классификация и выявление новизны;
9) построение ранговых зависимостей; 10) добыча данных.

Сферы применения

Целью машинного обучения является частичная или полная автоматизация человеческой деятельности в самых разных областях.

Распознавание речи – преобразование голосового сигнала в цифровую информацию, например, текст или запрос для поискового сервера. Обратной задачей является синтез речи.

Распознавание жестов – преобразование жестов в цифровую информацию: текст, клавиатурные команды. Распознавание эмоций и мимики.

Распознавание рукописных текстов – преобразование рукописного текста в цифровую информацию.

Распознавание образов и, в частности, компьютерное зрение – классификация и идентификация объектов по характерным конечным наборам свойств и признаков.

Техническая диагностика – определение технического состояния объектов.

Медицинская диагностика – процесс установления диагноза, т.е. заключения о сущности болезни и состоянии пациента. Анализ данных с сенсоров.

Прогнозирование временных рядов – предсказание будущих значений временного ряда по настоящим и прошлым значениям.

Биоинформатика – междисциплинарная наука, использующая методы прикладной математики, статистики и информатики в биохимии, биофизике, экологии, геномике и в других областях.

Обнаружение мошенничества – автоматическое обнаружение противоправных действий.

Обнаружение спама – обнаружение массовой рассылки корреспонденции рекламного или иного характера лицам, не выражавшим желания её получать.

Категоризация документов – отнесении документа к одной из нескольких категорий на основании содержания документа.

Биржевой технический анализ – прогнозирование вероятного изменения цен на основе закономерностей изменений цен в прошлом в аналогичных обстоятельствах.

Финансовый надзор – это деятельность уполномоченных органов, направленная на исполнение требований законодательства органами государственной власти, органами местного самоуправления, их должностными лицами, юридическими лицами и гражданами с целью выявления, пресечения и предупреждения правонарушений, обеспечения законности и финансовой дисциплины.

Кредитный скоринг – система оценки кредитоспособности (кредитных рисков) лиц, основанная на численных статистических методах.

Прогнозирование ухода клиентов – прогнозирование потери клиентов, выраженное в отсутствии покупок или платежей в течение определенного периода времени для компаний с подписной и транзакционной моделью бизнеса (банки, операторы связи, SaaS-сервисы), подразумевающих регулярные платежи в сторону компании.

Хемоинформатика (химическая информатика, молекулярная информатика) – применение методов информатики для решения задач химии и синтеза новых соединений.

Обучение ранжированию в информационном поиске – увеличение качества поиска, создание рекомендательных систем, оценка качества найденной информации.

Навигация и контроль действий – помощь водителям транспортных средств, а также беспилотные транспортные средства, автоматический контроль транспортных потоков.

Домашняя автоматизация – система домашних устройств, способных выполнять действия и решать определенные повседневные задачи без участия человека.

Машинное обучение бурно развивается, поэтому постоянно появляются новые не перечисленные здесь сферы применения.

Краткая история

Термин «машинное обучение» в 1959 году ввёл исследователь в области компьютерных игр Артур Самуэль в своей работе «Некоторые исследования в области Машинного Обучения с использованием игры в шашки» [1.4] и определил его как «процесс, в результате которого машина (компьютер) способна показывать поведение, которое в неё не было явно заложено (запрограммировано)». Игру в шашки, изобретенную Самуэлем в 1952 году, принято считать первой программой, способной самообучаться. Самуэль выбрал шашки, потому что правила игры относительно просты, но имеют развитую стратегию.

Эффективность машинного обучения в решении задач была продемонстрирована достаточно давно: еще в 1936 году знаменитый английский статистик Рональд Фишер сумел научить компьютер определять вид ириса по ширине цветка и чашелистика.

В тридцатые годы 20 века Карел Чапек изобрел термин «робот», в сороковые годы Айзек Азимов сформулировал законы робототехники, но первым, кто перевёл проблему «интеллектуальных машин» из научной фантастики в разряд прикладных проблем был математик Алан Тьюринг. В 1950 году в своей работе «Вычислительные машины и разум» [1.5] он рассмотрел вопрос «Могут ли машины думать?», но так как термины «машины» и «думать» не могут быть определены однозначно, Тьюринг предложил заменить вопрос на другой, тесно связанный с первым, но выраженный не такими двусмысленными понятиями: может ли машина совершать действия, неотличимые от обдуманных действий. С помощью такой постановки вопроса можно избежать сложных философских проблем по определению терминов «думать», «мышление» и сосредоточить внимание на решении практических задач.

Заменив философский вопрос на прикладной, Тьюринг предложил для проверки возможностей компьютерной программы свой знаменитый Тест Тьюринга. Стандартная интерпретация этого теста звучит следующим образом: «Человек взаимодействует с одним компьютером и одним человеком. На основании ответов на вопросы он должен определить, с кем он разговаривает: с человеком или компьютерной программой. Задача компьютерной программы – ввести человека в заблуждение, заставив сделать неверный выбор». Однако Тьюринг говорит не об одурачивании людей, а о воспроизведении когнитивных способностей человека [1.6]. Хотя бы внешне.

Тест Тьюринга имеет недостатки:

• чрезмерный антропоморфизм (рисунок 1.5);
• непрактичность – самолёты не машут крыльями, как птицы, чтобы летать, а машины не обязаны имитировать поведение людей, чтобы решать прикладные задачи;
• возможность имитации «мышления» по неким механическим правилам, например, как в мысленном эксперименте «Китайская комната» Джона Сёрля (John Searle, 1980).

Рис. 1.5 – Поведение человека и разумное поведение

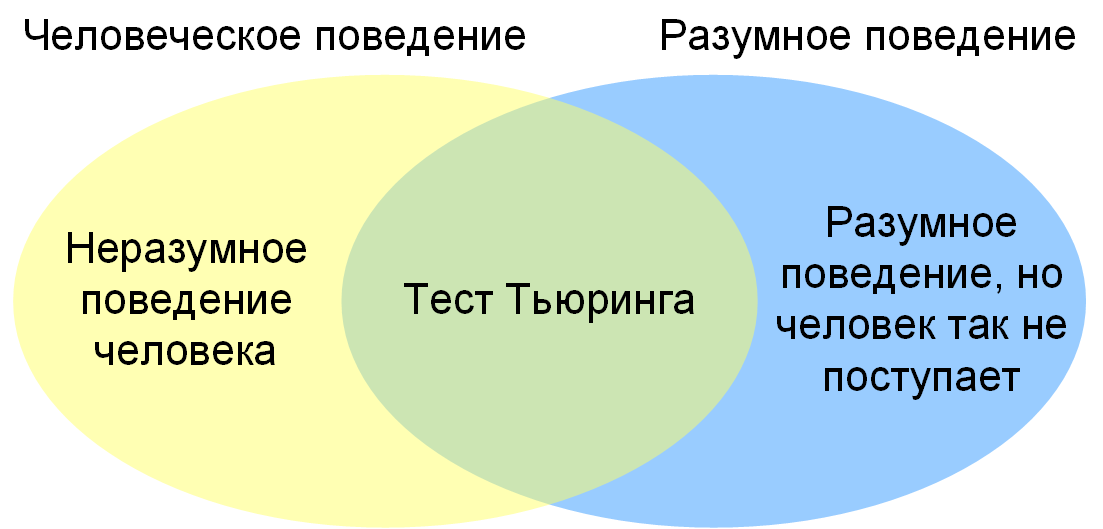
Несмотря на обоснованную критику, тест Тьюринга задаёт правильное направление мысли, а именно: не важно, думает машина или нет, потому что нет однозначного определения слов «думать» или «интеллект», главное, что машина может справляться с поставленными перед ней сложными задачами, например, имитировать поведение человека.

Современный интерес к машинному обучению возрос после того, как искусственные нейронные сети вновь стали популярными. Искусственная нейронная сеть (ИНС) – это математическая модель, а также её программное или аппаратное воплощение, построенная по принципу организации и функционирования биологических нейронных сетей, т.е. сетей нервных клеток живого организма. Необязательно, чтобы строение ИНС и мозга совпадали. В ИНС воплощены идеи коннекционизма, т.е. моделирования мыслительных или поведенческих явлений в сетях из связанных между собой простых элементов.

Первой попыткой построить ИНС по принципу функционирования мозга были нейронные сети Уоррена Мак-Каллока и Уолтера Питтса, описанные в статье 1943 года «Логическое исчисление идей, относящихся к нервной активности» [1.7, 1.8]. По примеру классических философов Греции они попытались математически смоделировать работу мозга. Это была яркая идея, учитывая то, что электрическая природа сигналов нейронов будет продемонстрирована только спустя семь лет в конце 1950-х годов. Математическая модель сети Мак-Каллока и Питтса из искусственных нейронов (рисунок 1.6) теоретически могла выполнять числовые или логические операции любой сложности.

Рис. 1.6 – Схема искусственного нейрона:
1) нейроны, выходные сигналы которых поступают на вход данному;
2) ω_i – веса входных сигналов; 3) сумматор входных сигналов;
4) вычислитель передаточной (активационной) функции;
5) нейроны, на входы которых подаётся выходной сигнал данного

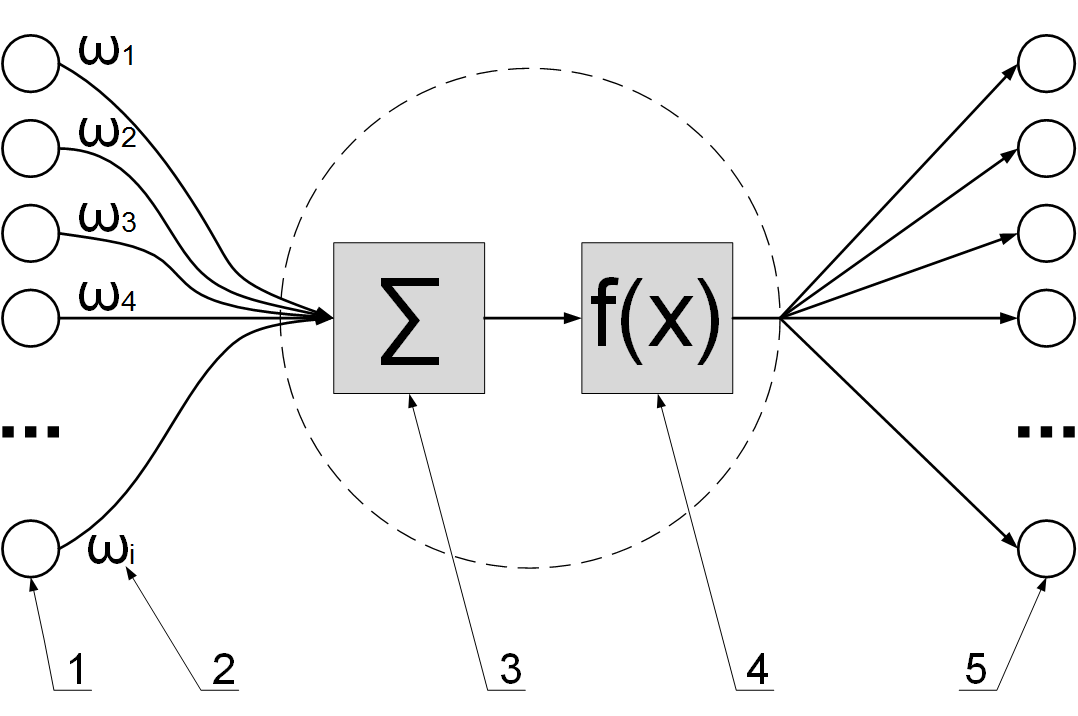
На вход искусственного нейрона поступают импульсы от произвольного числа других нейронов сети. Связи, по которым выходные сигналы одних нейронов поступают на входы других, часто называют синапсами по аналогии со связями между биологическими нейронами. Каждая связь характеризуется своим весом. Связи с положительным весом называются возбуждающими, а с отрицательным – тормозящими. Нейрон имеет один выход, часто называемый аксоном по аналогии с биологическим прототипом. С единственного выхода нейрона сигнал может поступать на произвольное число входов других нейронов. Если на выходе нейрона есть ненулевой сигнал (положительный или отрицательный), то говорят, что нейрон активен или возбуждён.

В сумматоре поступающие импульсы на вход нейрона умножаются на веса входов и слаживаются:

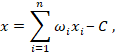(1.1)

где n – количество входящих синапсов; ω_i – веса входов (положительные возбуждающие или отрицательные тормозящие); x_i – сигналы на входах; C – константа для формирования порога чувствительности нейрона, которая называется сдвиг (bias). Функция x называется индуцированным локальным полем нейрона или взвешенной суммой. Возможные значения сигналов на входах нейрона x_i считают заданными в интервале [0,1]. Сигналы на входах, в зависимости от архитектуры сети, могут быть либо дискретными (только 0 или только 1), либо аналоговыми (непрерывными в интервале от 0 до 1 включительно).

Затем к индуцированному локальному полю нейрона x (см. формулу 1.1) применяется функция, называемая передаточной функцией ƒ(x) или функцией активации, функцией срабатывания, которая определяет зависимость сигнала на выходе нейрона от взвешенной суммы сигналов на его входах. Использование различных передаточных функций позволяет вносить нелинейность в работу нейрона и в целом нейронной сети. Без этой нелинейности нейронная сеть вырождается в задачу линейной алгебры, т.е. в обычное перемножение матриц и векторов.

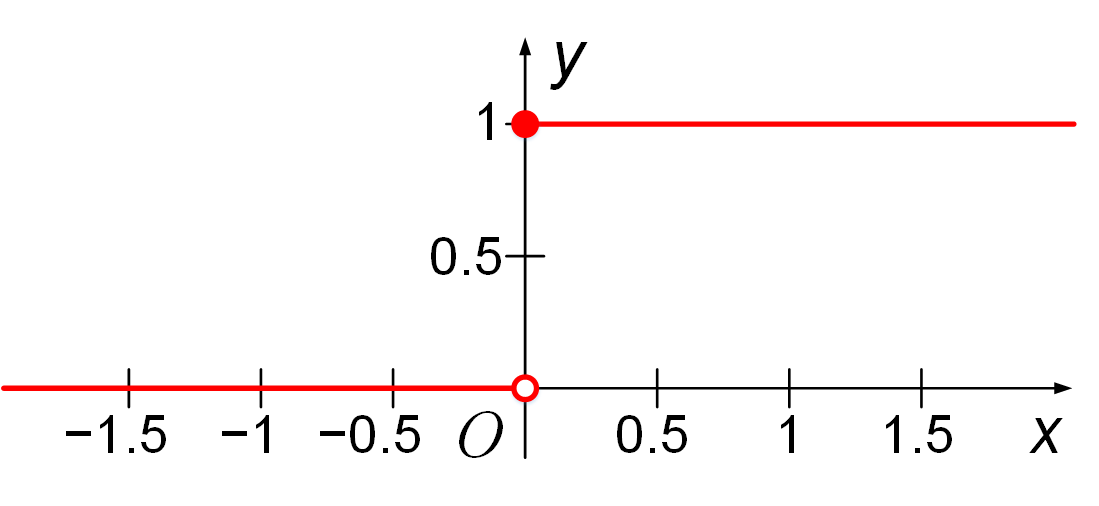
Существует множество различных передаточных функций. Самой известной передаточной функцией является функция Хевисайда (рисунок 1.7), которая представляет собой перепад (ступеньку) и записывается формулой:

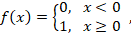(1.2)

где переменная x является индуцированным локальным полем (взвешенной суммой с порогом) и вычисляется по формуле (1.1).

Рис. 1.7 – График функции Хевисайда, одной из передаточных функций

Построения Мак-Каллока и Питтса были теоретическими, а в 1951 году Марвин Минский и Дин Эдмондс создают первую машину на нейронной сети: стохастический нейронный аналоговый калькулятор с подкреплением (Stochastic Neural Analog Reinforcement Calculator, SNARC). Машина состояла из 40 искусственных нейронов, соединённых в случайном порядке, была размером с рояль и с помощью обучения с подкреплением моделировала поведение крысы в лабиринте в поисках пищи. С помощью SNARC Марвин Минский проверял теорию Хебба о нейропластичности.

В 1957 году Фрэнк Розенблатт изобретает перцептрон (от лат. perсeptio – восприятие) – математическую и компьютерную модель восприятия информации мозгом (кибернетическую модель мозга) [1.9]. Изучая нейронные сети типа перцептрона, Розенблатт хотел «понять фундаментальные законы организации, общие для всех систем обработки информации, включая как машины, так и человеческий разум». Перцептрон и, в частности, элементарный перцептрон состоит из трёх типов элементов и связей между ними (рисунок 1.8):

Рис. 1.8 – 1) схема перцептрона с тремя выходами;
2) элементарный перцептрон имеет только один выход

Сигналы на перцептрон поступают от S-элементов («S» от англ. «Sensor» – сенсор). S-элементы выдают дискретный сигнал: либо 1, либо 0. S-элементы не являются нейронами, потому что не обучаются, т.е. не меняют веса связей с нейронами. Внутри S-элементов есть датчик, сенсор или рецептор. От воздействия какого-либо из видов энергии (например, свет, звук, давление, тепло и т.п.) датчик внутри S-элемента вырабатывает сигнал. Если сигнал от датчика превышает некоторый порог, то на выходе S-элемента получается сигнал +1, иначе – 0 (нет сигнала). Поведение S-элемента описывается функцией Хевисайда (1.2) с некоторым порогом срабатывания C (см. формулу 1.1).

S-элементы соединяются синапсами, S–A связями, с A-элементами. Веса S–A связей могут иметь три дискретных значения: (–1) (тормозящий синапс), (+1) (возбуждающий синапс) и 0 (отсутствие синапса, когда нет физической связи между сенсором S и нейроном A). S–A связи выбираются случайным, но фиксированным образом, т.е. не меняются во время обучения и работы сети.

A-элементы («A» от англ. «Associative» – ассоциативный) называются ассоциативными, потому что каждому такому элементу, как правило, соответствует целый набор (ассоциация) S-элементов. A-элементы являются искусственными нейронами (см. рисунок 1.6). Передаточной функцией (функцией активации) нейрона для A-элементов является функция Хевисайда (1.2). Таким образом, A-элемент активизируется, как только взвешенная сумма сигналов от S-элементов на его входе превысит некоторую пороговую величину C (см. формулу 1.1), и индуцированное локальное поле нейрона станет больше либо равным нулю: x ≥ 0. В соответствии с функцией Хевисайда, выходной сигнал ассоциативных нейронов является дискретным: либо 0 (нет сигнала), либо 1 (есть сигнал).

A-элементы соединяются синапсами (A–R связями) с R-элементами. Сигнал от i-того ассоциативного элемента передаётся в j-тый реагирующий элемент с коэффициентом W_i,j. Этот коэффициент называется весом A–R связи. Веса A–R связей W_i,j могут быть любыми (являются вещественными числами). A–R связи выбираются случайным, но фиксированным образом, т.е. не меняются во время обучения и работы сети. Обучение перцептрона состоит в изменении весовых коэффициентов W_i,j.

R-элементы («R» от англ. «Reacting» – реагирующий) называются реагирующими, потому что эти нейроны выдают результат, реагируют на входные импульсы от сенсоров. R-элементы являются искусственными нейронами (см. рисунок 1.6). Реагирующий элемент выдаёт выходной дискретный сигнал: (+1), если сумма значений входных сигналов, помноженных на веса, является строго положительной; (–1), если сумма значений входных сигналов, помноженных на веса, является строго отрицательной. Если сумма значений входных сигналов, помноженных на веса, равна нулю, то выход можно считать либо равным нулю, либо неопределённым. Таким образом, передаточной функцией (функцией активации) нейрона для R-элементов является сигнум функция (сигнум, от лат. «signum» – знак):

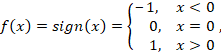(1.3)

где x является индуцированным локальным полем нейрона и вычисляется по формуле (1.1). График сигнум функции изображён на рисунке 1.9.

Рис. 1.9 – График сигнум функции sign(x)

Согласно современной терминологии классический перцептрон является искусственной нейронной сетью:

• с одним скрытым слоем, трёхслойный по классификации Розенблатта и двухслойный по современной системе обозначений с той особенностью, что первый слой не обучаемый;
• с пороговой функцией активации Хевисайда (1.2) для ассоциативных нейронов и сигнум функцией активации (1.3) для реагирующих нейронов;
• с прямым распространением сигнала (без обратной связи).

Классический метод обучения перцептрона – это обучение с коррекцией ошибки, специальный итерационный метод обучения проб и ошибок, который напоминает процесс обучения человека. Представляет собой такой метод обучения с учителем, при котором вес W_i,j связи A–R не изменяется до тех пор, пока текущая реакция перцептрона остаётся правильной. При появлении неправильной реакции вес изменяется на единицу, а знак изменения (+1 или –1) определяется противоположным от знака ошибки. Например, мы хотим обучить элементарный перцептрон (см. рисунок 1.8.2) разделять два класса объектов, круги и квадраты, так, чтобы при предъявлении объектов первого класса (круги) выход перцептрона был положителен (+1), а при предъявлении объектов второго класса (квадраты) – отрицательным (−1). Для этого выполним следующий алгоритм:

1. Случайным образом выбираем пороги C (см. формулу 1.1) для A-элементов. Случайным образом устанавливаем связи S–A. Далее пороги и связи не изменяются. Все A-элементы элементарного перцептрона соединены одной A–R связью с единственным выходным R-элемента (см. рисунок 1.8.2).
2. Начальные коэффициенты W_i полагаем равными нулю.
3. Предъявляем обучающую выборку: круги и квадраты с указанием класса, к которым они принадлежат.
   1. Если предъявили круг и выход перцептрона положительный – ничего не делаем.
   2. Если предъявили квадрат и выход перцептрона отрицательный – ничего не делаем.
   3. Если предъявили круг и выход перцептрона отрицательный – к весу W_i каждого активного А-элемента прибавляется единица. Активный элемент тот, который выдаёт единицу на выходе. Если элемент не активный (ноль на выходе), то единица к весу этого элемента не прибавляется.
   4. Если предъявили квадрат и выход перцептрона положительный – от веса W_i каждого активного A-элемента отнимается единица.
4. Шаг 3 выполним для всей обучающей выборки. В результате обучения сформируются значения весов A–R связей W_i.

В книге 1962 года «Принципы нейродинамики: Перцептроны и теория механизмов мозга» [1.10] Розенблатт сформулировал и доказал теорему о сходимости перцептрона: элементарный перцептрон, обучаемый по методу коррекции ошибки (с квантованием или без него), независимо от начального состояния весовых коэффициентов и порядка показа образцов из обучающей выборки всегда научится различать два класса объектов за конечное число шагов, если только существует такая классификация. Также в книге рассматриваются:

• многослойные перцептроны с дополнительными слоями A-элементов;
• перцептроны с перекрёстными связями, т.е. со связями между элементами одного слоя;
• перцептроны с обратными связями, которые согласно современной классификации относится к рекуррентным нейронным сетям (RNN);
• обучение без учителя или альфа-система подкрепления – это система подкрепления, при которой веса всех активных связей W_i,j, которые ведут к элементу u_j, изменяются на одинаковую величину, а веса неактивных связей за это время не изменяются.

Сначала перцептрон был реализован, как компьютерная программа, а впоследствии в 1960 году, как электронное устройство – нейрокомпьютер Марк-1. Классификатор визуальных образов Марк-1 имел входной (сенсорный) слой из 400 светочувствительных S-элементов в сетке 20х20 (400 пикселей), моделирующий небольшую сетчатку, как светочувствительные клетки сетчатки глаза или фоторезисторы матрицы камеры. Далее был слой ассоциации из 512 A-элементов, сделанных с применением шаговых двигателей. Каждый из A-элементов мог принимать несколько возбуждающих и тормозящих входов от S-элементов. После слоя ассоциации располагался выходной (ответный) слой из восьми R-элементов. Сенсорный слой случайным образом соединялся с ассоциативным слоем с помощью S–A связей на специальной приборной доске, но после установки соединения все S–A связи оставались неизменными до конца эксперимента. A–R связи между ассоциативным и выходным слоями имели переменные веса (потенциометры с двигателем). Переменные веса корректировались с помощью метода коррекции ошибки. Нейрокомпьютер Марк-1 состоял из шести стоек электронного оборудования и занимал примерно 3,4 м2 площади. Марк-1 был способен распознавать некоторые буквы английского алфавита, написанные на карточках, которые подносили к его «глазам» из 400 фотосенсоров.

В 1969 году вышла книга Марвина Минского (того самого, который сделал первый нейрокомпьютер SNARC) и Сеймура Паперта «Перцептроны» [1.11], в которой были математически доказаны ограничения перцептронов. Было показано, что перцептроны принципиально не в состоянии выполнять многие из тех функций, которые хотели от них получить. Минский показал преимущество последовательных вычислений перед параллельными в определённых классах задач. В то время была слабо развита теория о параллельных вычислениях, а перцептрон полностью соответствовал принципам параллельных вычислений. Некоторые ограничения перцептрона показаны на рисунке 1.10.

Рис. 1.10 – Ограничения перцептрона:
1) Это одна и та же буква? 2) Это один и тот же текст?
3) Из какого количества частей состоит фигура?
4) Внутри какого объекта нет другой фигуры?
5) Какая фигура внутри объектов повторяется два раза?

Основными недостатками классического перцептрона являются:

• трудности с распознаванием объекта, над которым провели операции переноса, поворота, растяжения-сжатия (рисунки 1.10.1 и 1.10.2);
• неспособность решать задачи на определение «связности» фигур (рисунки 1.10.3, 1.10.4 и 1.10.5).

В начале 60-х годов многими математиками в рамках теории управления были заложены основы метода обратного распространения ошибки (backpropagation), который необходим для глубокого обучения (Deep Learning) [1.12]. Однако метод обратного распространения ошибки не применялся непосредственно к нейронным сетям до 80-х годов.

В процессе своего развития машинное обучение пережило две «зимы искусственного интеллекта». Зимой искусственного интеллекта называется период сниженного общественного интереса и существенного уменьшения финансирования исследований в этой области со стороны бизнеса и государственных организаций. Различают две зимы 1974–1980 и 1987–1993 годов, а также несколько меньших периодов, связанных с провалами крупных проектов в этой области. Несмотря на низкое финансирование, исследования в области машинного обучения продолжались. Часто под другими названиями.

Модели машинного обучения

В машинном обучении существует огромное количество различных моделей, самыми популярными из которых являются:

• метод опорных векторов (support vector machine, SVM);
• метод k-ближайших соседей (k-nearest neighbors, k-NN);
• дерево принятия решений (decision tree) и случайный лес (random forest);
• гауссовский процесс (Gaussian process);
• байесовская теория классификации;
• эволюционные алгоритмы, которые моделируют процессы естественного отбора;
• алгоритмы усиления (бустинга): AdaBoost, BrownBoost, CoBoost и т.д.;
• ансамблевое обучение (ensemble learning);
• марковские процессы;
• мешок слов;
• метод главных компонент (principal component analysis, PCA);
• искусственные нейронные сети;
• линейная и логистическая регрессии;
• метод k-средних (k-means);
• и др.

Список литературы

1.1. Box G.E.P., Hunter W.G., Hunter J.S., ″Statistics for Experimenters: Design, Innovation, and Discovery,″ John Wiley & Sons, Hoboken, 2 ed., 2005, p. 664. ISBN: 978-0471718130.

1.2. O. Duchenne, J. Y. Audibert, R. Keriven, J. Ponce and F. Segonne, ″Segmentation by transduction,″ 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, 2008, pp. 1-8, doi: 10.1109/CVPR.2008.4587419

1.3. Дюк В.А., Флегонтов А.В., Фомина И.К. Применение технологий интеллектуального анализа данных в естественнонаучных, технических и гуманитарных областях // Известия Российского государственного педагогического университета им. А.И. Герцена. 2011. No 138. С. 77-84.

1.4. Samuel A.L., ″Some Studies in Machine Learning Using the Game of Checkers,″ in IBM Journal of Research and Development, Vol. 3, No. 3, July 1959, pp. 210-229, doi: 10.1147/rd.33.0210.

1.5. Turing A.M., ″Computing machinery and intelligence,″ Oxford University Press on behalf of the Mind Association, Mind, New Series, Vol. 59, No. 236, Oct., 1950, pp. 433–460.

1.6. Harnad S., ″The Turing Test Is Not A Trick: Turing Indistinguishability Is A Scientific Criterion,″ SIGART Bulletin, No. 3(4), October, 1992, pp. 9–10.

1.7. McCalloch W.S., Pitts W., ″A Logical Calculus of Ideas Immanent in Nervous Activity,″ Bulletin of Mathematical Biophysics, Vol. 5, 1943, pp. 115–133, doi: 10.1007/BF02478259

1.8. Мак-Каллок У.С., Питтс В. Логическое исчисление идей, относящихся к нервной активности // В сб. «Автоматы» под ред. К.Э. Шеннона и Дж. Маккарти. – М.: Изд-во иностр. лит., 1956. – С. 363–384. (Перевод английской статьи 1943 г.)

1.9. Rosenblatt F., ″The perceptron: A probabilistic model for information storage and organization in the brain,″ Psychological Review, Vol. 65, No. 6, 1958, pp. 386–408, doi: 10.1037/h0042519

1.10. Rosenblatt F., ″Principles of neurodynamics: Perceptions and the theory of brain mechanism,″ Spartan Books, Washington, DC, 1962, p. 616.

1.11. Marvin L. Minsky, Seymour A. Papert, ″Perceptrons: expanded edition,″ MIT Press Cambridge, MA, USA, 1988, p. 292. ISBN: 0-262-63111-3.

1.12. Schmidhuber J., ″Deep learning in neural networks: An overview,″ Neural Networks, Vol. 61, 2015, pp. 85–117, doi: 10.1016/j.neunet.2014.09.003

Глава 2. Введение в искусственные нейронные сети

Принципы работы искусственных нейронных сетей

Обзор основных архитектур ИНС

Одной из моделей машинного обучения являются искусственные нейронные сети (ИНС). В настоящее время происходит возрождение ИНС под новым брендом «глубокое обучение» (Deep Learning). ИНС являются иерархическими классификаторами, которые способны самостоятельно выделять признаки в исходном сигнале. Общим показателем ИНС является количество скрытых слоёв. Некоторые современные сети имеют сотни и даже тысячи скрытых слоёв. Выделяют большое множество (зоопарк) архитектур ИНС. Перечислим самые популярные из них.

Сети без обратных связей или сети прямого распространения сигнала, в которых сигнал переходит от выходов нейронов i-того слоя ко входам нейронов (i+1)-го слоя и не возвращается на предыдущие слои:

• перцептроны (однослойные, многослойные с перекрёстными связями и т.д.), кроме перцептронов с обратными связями;
• байесовская нейронная сеть;
• экстремальная обучающаяся машина (extreme learning machine);
• фактически, любая ИНС, которая является направленным ациклическим (без циклов) графом.

Свёрточные нейронные сети (Convolutional Neural Networks, CNN, ConvNets), отличительной особенностью которых является операция свёртки (конволюция):

• AlexNet [2.1];
• LeNet-5 [2.2];
• свёрточные сети с выделением области (Region Based CNNs, R-CNN) [2.3];
• развёртывающие нейронные сети (deconvolutional networks, DN, DeConvNet) или обратные графические сети, свёрточные сети наоборот [2.4].

Генеративные состязательные сети (Generative adversarial networks, GAN) [2.5], которые состоят из двух конкурирующих ИНС: генеративной модели, генерирующей образцы, и дискриминативной модели, пытающейся отличить правильные («подлинные») образцы от неправильных. GAN достаточно сложно обучить, потому что задачей является не просто обучение двух сетей, но и соблюдение баланса, равновесия между ними. Если одна из сетей (генератор или дискриминатор) станет намного лучше другой, то GAN не будет сходиться (обучаться).

Рекуррентные нейронные сети (Recurrent Neural Networks, RNN) [2.6, 2.7, 2.8] или сети с памятью. Содержат нейроны, которые в процессе работы могут сохранять информацию о своих предыдущих состояниях, такие нейроны получают информацию не только от предыдущего слоя, но и от самих себя в результате предыдущего прохода. Рекуррентные сети являются нейросетевым воплощением цепей Маркова. Различают множество архитектур рекуррентных ИНС:

• сеть с долговременной и кратковременной памятью (Long Short Term Memory, LSTM);
• полностью рекуррентная сеть;
• рекурсивная сеть;
• нейронная сеть Хопфилда, один из видов полносвязных ИНС;
• машина Больцмана и ограниченная машина Больцмана;
• нейронная сеть Хэмминга;
• двунаправленная ассоциативная память (BAM) или нейронная сеть Коско;
• двунаправленные рекуррентные ИНС (bidirectional recurrent neural networks);
• сети Элмана и Джордана;
• эхо-сети и импульсные (спайковые) нейронные сети;
• машины неустойчивых состояний (liquid state machines, LSM);
• нейронный компрессор истории;
• рекуррентные сети второго порядка;
• управляемые рекуррентные нейроны (Gated Recurrent Units, GRU);
• нейронные машины Тьюринга (Neural Turing machines, NTM) и т.д.

Автокодировщики, задачей которых является получение на выходном слое отклика, наиболее близкого к входному. По этой причине выходной слой автокодировщика должен содержать столько же нейронов, сколько и входной слой. Сеть напоминает по форме песочные часы, так как скрытые слои автокодировщиков меньше, чем входной и выходной слои. Различают следующие автокодировщики:

• ванильный автокодировщик (Vanilla autoencoder);
• многослойный автокодировщик;
• свёрточный автокодировщик;
• упорядоченный автокодировщик (regularized autoencoder);
• разреженный автокодировщик;
• шумоподавляющий (помехоустойчивый) автокодировщик (denoising autoencoder, DAE).

Глубокие нейронные сети, которые отличаются от просто нейронных сетей наличием большого количества скрытых слоёв:

• глубокие сети доверия (Deep Belief Networks, DBN), которые являются первыми глубокими сетями;
• глубокая остаточная нейронная сеть (Residual neural network, ResNet) [2.9], которая является попыткой смоделировать пирамидальные нейроны в коре больших полушарий;
• глубокая машина Больцмана (Deep Boltzmann Machine, DBM);
• размещённые друг над другом автокодировщики (Stacked Auto-Encoders);
• глубокие свёрточные нейронные сети (Deep Convolutional Neural Networks, DCNN), глубокие свёрточные обратные глубинные сети (Deep Convolutional Inverse Graphics Networks, DCIGN) [2.10], VGG Net [2.11] и т.д.

Нейронные сети Кохонена, у которых основным элементом является слой Кохонена. В этом слое выходные сигналы обрабатываются по правилу «победитель получает всё», т.е. наибольший сигнал превращается в единичный, а остальные обращаются в ноль:

• сети векторного квантования (learning vector quantization);
• самоорганизующиеся карты Кохонена;
• упругие карты.

Сети радиально-базисных функций (radial basis function networks), которые использует радиальные базисные функции в качестве функций активации.

Смешанные нейронные сети, которые совмещают в себе различные архитектуры для большей эффективности:

• GoogLeNet;
• AlphaGo и т.д.

Этот список не является исчерпывающим. Постоянно появляются новые архитектуры. Более того, вышеизложенное разделение ИНС на архитектуры является условным, так как нет чётких границ. Например, свёрточная ИНС одновременно является сетью без обратных связей, она же глубокая нейронная сеть, а также она может являться автокодировщиком или частью более сложной архитектуры. К сожалению, в этой главе нет возможности подробно описать архитектуру каждой сети. Однако все ИНС используют общие принципы работы и имеют схожие проблемы обучения, кратко рассмотренные ниже.

Существует множество программных библиотек для машинного обучения и обучения ИНС: TensorFlow, Theano, Keras, Torch, Caffe, MXNet, Matlab Neural Networks Toolbox, Wolfram Mathematica и др.

Функции активации нейрона

В предыдущей главе были рассмотрены две ступенчатые функции активации перцептрона: функция Хевисайда (1.2) и сигнум-функция (1.3). В современных ИНС широко применяется метод обратного распространения ошибки (backpropagation), в котором используется производная от функции активации. Но ступенчатые функции не дифференцируемы, т.е. не имеют производной на ступеньке. Поэтому при использовании метода обратного распространения ошибки применяются другие функции активации. В таблице 2.1 показаны несколько самых широко применяемых в ИНС функций активации.

Таблица 2.1 – Функции активации нейрона в ИНС

№	Название	Формула	Изображение
1	Rectified linear unit (ReLU)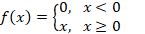
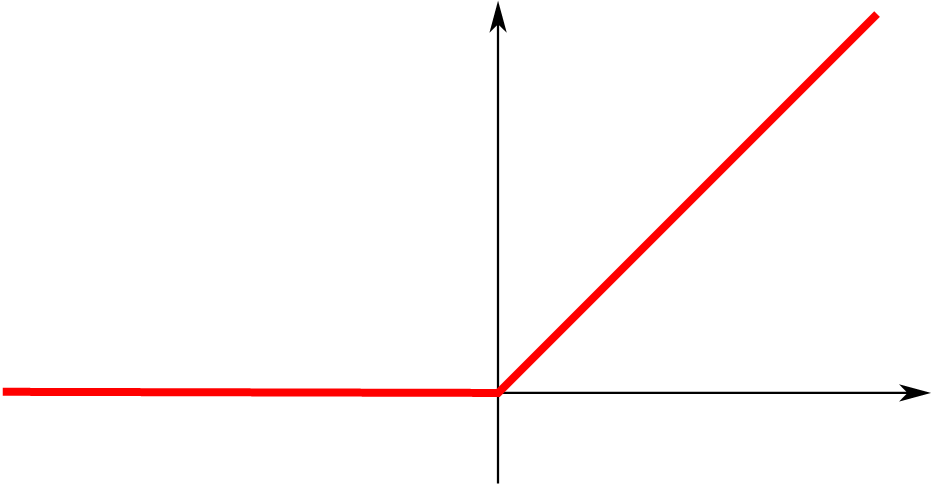2	Параметрический rectified linear unit (PReLU)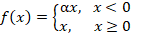
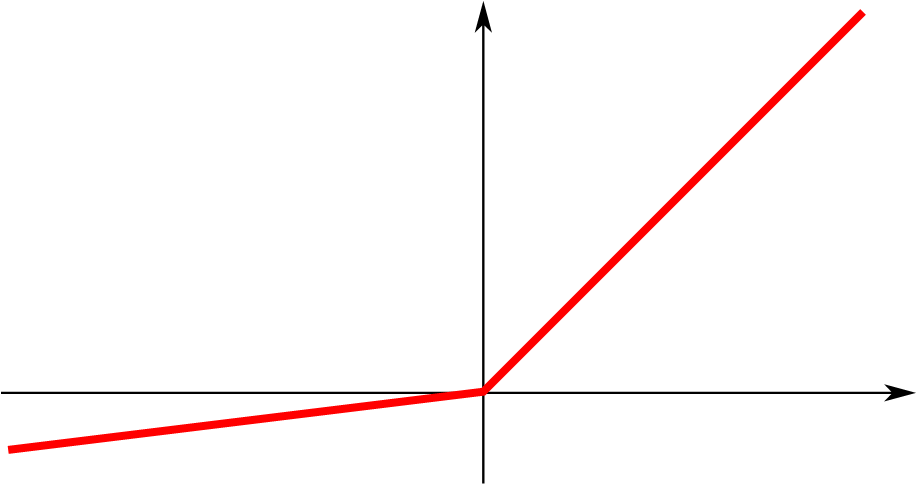3	Логистическая функция или сигмоида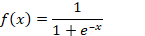
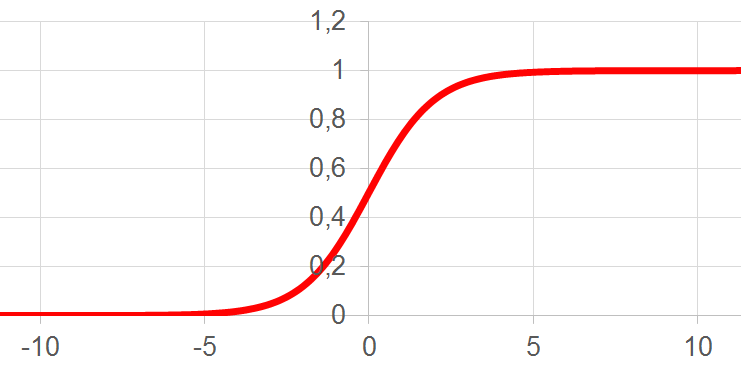4	Гиперболический тангенс (TanH)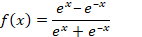
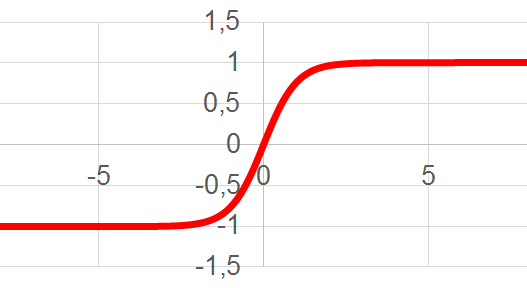5	Арктангенс (ArcTan)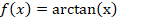

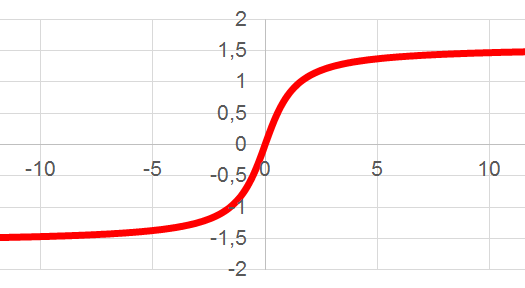Здесь аргумент активационной функции x – это взвешенная сумма (1.1) или индуцированное локальное поле; α во второй строке таблицы 2.1 – это малый коэффициент, обычно равный α = 0,01. Малый коэффициент α нужен, чтобы производная функции ReLU не была равна нулю при x < 0. Однако наличие малого коэффициента α некритично, как может показаться, так как вероятность того, что активационные функции всех нейронов ИНС станут равными нулю крайне мала. Например, в одномерном случае невозможно преодолеть гору, в двумерном случае гору можно обойти слева или справа, а в многомерном N-мерном пространстве существует множество путей обхода препятствий, и чем больше измерений, тем меньше вероятность попасть в локальный минимум.

Функция ReLU (строка 1 таблицы 2.1) была впервые применена в свёрточных ИНС для устранения проблемы исчезающего градиента и доказала свою эффективность. В отличие от сигмоиды и гиперболического тангенса, операция ReLU гораздо быстрее, при этом качество обучения снижается незначительно. Поэтому ReLU на данный момент является самой популярной активационной функцией в свёрточных ИНС.

Функция активации необходима для внесения нелинейности в систему. Без нелинейности ИНС будет вырождаться в обычное перемножение матриц и векторов, т.е. в линейную алгебру. В данном контексте уместно напомнить общеизвестный факт о том, что никакие линейные преобразования пространства признаков не позволяют улучшить качество классификации, т.е. линейная разделимость объектов в пространстве признаков является неэффективной. С помощью линейных преобразований невозможно решить нетривиальные задачи, например, разделить пересекающиеся множества.

Свёрточные ИНС

Для анализа изображений чаще всего используются свёрточные ИНС. Свёрточная ИНС была предложена и популяризована Яном Лекуном в 1988 году для распознавания изображений. Отличительной чертой свёрточных ИНС является операция свёртки.

Как известно, цветные RGB изображения 256 на 256 пикселей, можно представить, как матрицу 256×256×3 из 256 строк, 256 столбцов и толщиной 3 слоя. При операции свёртки каждый пиксель такого изображения умножается на матрицу (ядро или фильтр) свёртки, а результат суммируется и записывается в аналогичную позицию выходного изображения. По сути операция свёртки – это всё та же взвешенная сумма нейрона ∑ на рисунке 1.6, только выполняемая особым образом (рисунок 2.1), где значения матрицы свёртки – это веса синапсов w_i, значения пикселей изображения – это значения входящих сигналов нейрона x_i, а результатом является один пиксель нового изображения, в котором пиксели будут являться взвешенными суммами ∑w_i*x_i‒C (см. формулу 1.1).

Рис. 2.1 – Операция свёртки для одного пикселя
нового изображения с нулевым порогом

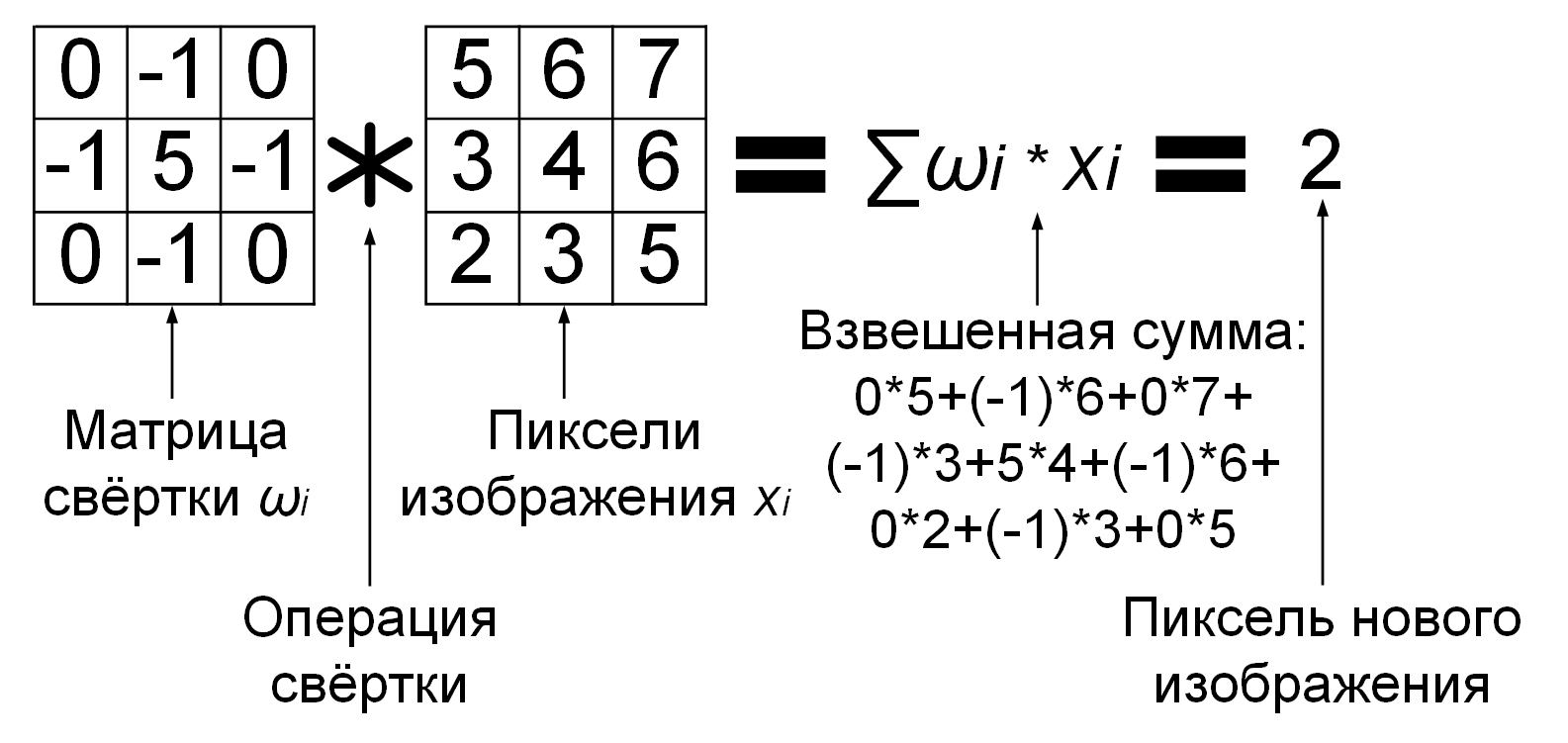
На рисунке 2.1 показана операция свёртки одного ядра размером 3×3 с нулевым порогом C (bias) с кусочком чёрно-белого изображения, т.е. изображения с глубиной один слой, в результате чего получается один пиксель нового обработанного изображения. Как правило, ядро свёртки передвигают на малое расстояние при движении по изображению. Например, ядро свёртки 3×3 обычно передвигают всего на один нейрон (пиксель), а ядро свёртки 5×5 передвигают на один–два нейрона (пикселя).

Глубина ядра свёртки всегда равна глубине обработанного изображения. Для исходного чёрно-белого изображения глубина равна 1, а для цветного RGB изображения глубина равна 3. Соответственно, на более глубоких свёрточных слоях глубина ядра свёртки увеличивается, потому что увеличивается глубина обработанного изображения. Таким образом для исходного цветного изображения матрица свёртки имеет глубину 3 и может быть равной: 3×3×3, либо 5×5×3, либо 7×7×3 и т.д. Обычно берут нечётное число для величины ядра свёртки, т.к. считается, что свёртка происходит вокруг центра, однако иногда встречаются свёрточные ИНС и с чётным размером ядер.

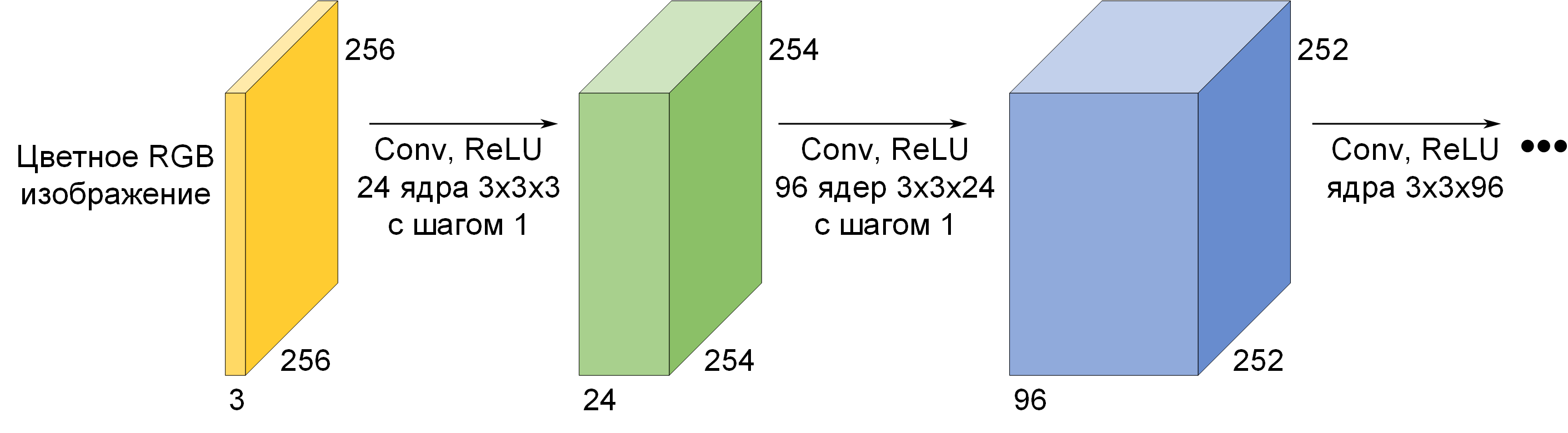
Результатом свёртки ядра 3×3×3 с шагом один со всем RGB изображением 256×256×3 будет новое изображение с матрицей 254×254×1, в котором значения пикселей будут являться взвешенными суммами. Если ядро свёртки размером 3×3×3, то нейрон имеет 27 синапсов (3*3*3=27), соединяющих его с 27 пикселями исходного изображения. Всего такой нейрон имеет 28 параметров, т.к. двадцать восьмой параметр – это порог C (bias).

Новая матрица имеет меньшее количество строк и столбцов 254, а не 256, из-за того, что ядро 3×3 не может выходить за пределы изображения. В общем случае длина и ширина матрицы уменьшаются на (k‒1) пиксель после каждой свёртки с единичным шагом, где k – это размер ядра. Иногда, для того, чтобы матрица не уменьшалась в размерах, вокруг изображения добавляют фаску (прокладку, zero padding) из нулей. Для ядра 3×3 с единичным шагом толщина фаски из нулей равна 1. Для ядра 5×5 с единичным шагом толщина фаски из нулей равна 2.

Несколько десятков таких ядер свёртки (фильтров) называют свёрточным слоем (convolutional layer). Свёрточный слой из N ядер превращает цветное RGB изображение 256×256×3 в матрицу 254×254×N значений. Такая матрица (или обработанное изображение) имеет глубину N, равную количеству ядер свёртки (количеству фильтров).

Веса ядер, т.е. значения матриц свёртки в свёрточном слое, не закладываются исследователем заранее, а вычисляются автоматически с помощью операции обратного распространения ошибки (backpropagation), которая будет рассмотрена далее.

Для улучшения работы ИНС применяется метод исключений (dropout), при котором проводится обучение ИНС с выбрасыванием случайных одиночных нейронов. Также для улучшения качества может применяться сеть в сети (network in network layer) – это ядро свёртки размером 1×1×N, где N – это количество ядер свёртки на предыдущем свёрточном слое, т.е. глубина матрицы. Сеть в сети была впервые применена в GoogLeNet.

Как и во всяком искусственном нейроне (см. рисунок 1.6), за взвешенной суммой ∑ следует функция активации. Для свёрточных ИНС функцией активации является функция ReLU (строки 1 и 2 таблицы 2.1) и её модификации (Noisy ReLU, Leaky ReLU и др.). Функция ReLU применяется к каждому значению матрицы 254×254×N.

Затем, как правило, применяется второй свёрточный слой из M ядер свёртки, который превратит матрицу 254×254×N в матрицу 252×252×M. При этом глубина ядер на втором свёрточном слое будет равна N и может быть равной: 3×3×N, либо 5×5×N, либо 7×7×N и т.д.

За вторым свёрточным слоем следует слой активации ReLU, т.е. функция ReLU применяется к каждому значению матрицы 252×252×M. Слой активации обычно логически объединяют со слоем свёртки (считают, что функция активации встроена в слой свёртки). На рисунке 2.2 показаны несколько слоёв свёртки и активации цветного изображения.

Рис. 2.2 – Несколько слоёв свёртки и активации цветного изображения

Другим важным аспектом свёрточных ИНС является операция пулинга (pooling) или субдискретизации, которая представляет собой нелинейное уплотнение карты признаков (рисунок 2.3).

Рис. 2.3 – Пулинг с функцией максимума, фильтром 2×2 и шагом 2

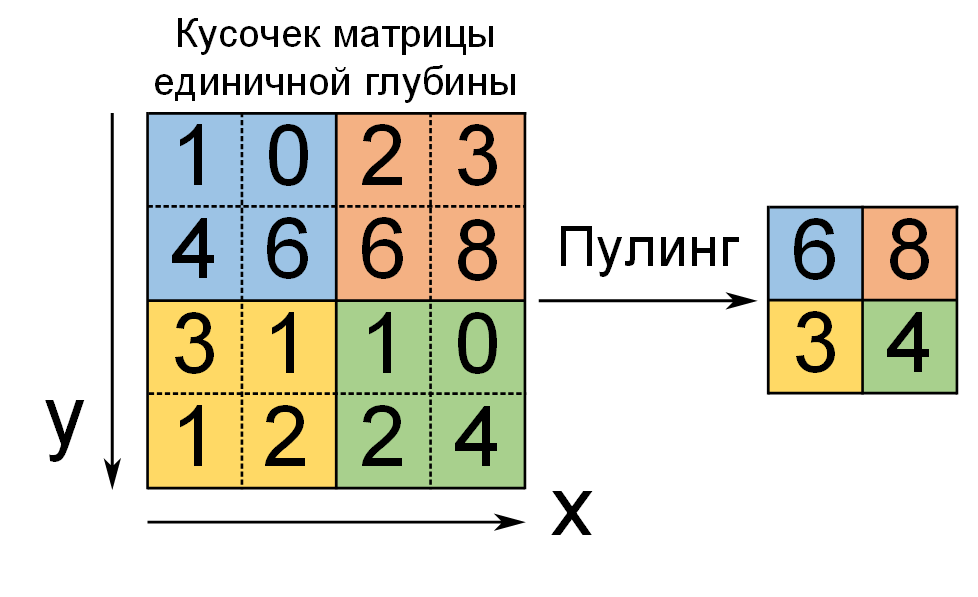
Операция пулинга позволяет существенно уменьшить пространственный объём изображения, сократить количество параметров и ускорить вычисления в сети и, как следствие, предотвратить переобучение. Считается, что если на предыдущем свёрточном слое уже были выявлены некоторые признаки, то для дальнейшей обработки такое подробное изображение уже не нужно, и оно уплотняется. При пулинге наличие признака важнее, чем его точная позиция на изображении. Слой пулинга вставляется между свёртками. Практика доказала преимущество пулинга с функцией максимума (maxpooling). При пулинге глубина матрицы остаётся неизменной, меняется только её длина и ширина. Ещё одним эффектом от пулинга является инвариантность (нечувствительность) распознавания к изменению размера изображения. Иногда исследователи полностью отказываются от пулинга, потому что утрачивается информация о точном местоположении признака.

Можно заметить, что функция ReLU неубывающая, а значит можно поменять местами слой активации и слой пулинга с функцией максимума, тем самым ускорив вычисления, но это уже вопрос оптимизации кода.

В самом конце свёрточная ИНС имеет полносвязные нейронные слои (fully connected layers). Полносвязная ИНС по своим свойствам является линейным классификатором. После нескольких прохождений свёртки и уплотнения изображение преобразуется в вектор признаков (дескриптор), который уникальным образом характеризует это изображение. Этот дескриптор подаётся на вход классификатора, где ему ставится в соответствие некий класс объектов, например, «кот» или «собака». Полносвязная ИНС может быть заменена на любой другой линейный классификатор (SVM, k-NN, логистическую регрессию, наивный байесовский классификатор и т.д.).

Классическая архитектура свёрточной ИНС выглядит так:

Свёрточная ИНС самонастраивается с помощью метода обратного распространения ошибки, автоматически меняет свои фильтры, и сама вырабатывает необходимую иерархию абстрактных признаков (последовательность карт признаков), фильтруя маловажные детали и выделяя существенное. Больше о том, что такое признаки (features), и как с ними работать, можно узнать в следующем разделе. Однако не пытайтесь понять и тем более изменить вырабатываемые автоматически признаки. При работе с ИНС разработчик должен сосредоточится на общей архитектуре сети и обучающих данных, чтобы улучшить результаты.

Исследователи заметили, что от слоя к слою признаки усложняются. Если на первом свёрточном слое сеть учится распознавать углы, линии, оттенки и особые точки, то на втором свёрточном слое это уже части объектов, например, части лиц. На третьем уровне уже можно выделить целые объекты: лица, предметы, текст. На более высоких уровнях появляются комбинации объектов и их зависимости, такие как книжная полка с книгами, группы лиц каких-нибудь музыкальных групп и т.д. (см. рисунок 2.4).

Рис. 2.4 – Автоматическое усложнение признаков в свёрточной ИНС [2.12]

Недостатком свёрточной ИНС является большое количество варьируемых параметров: число слоёв, размер ядра свёртки для каждого из слоёв, величина порога для взвешенной суммы свёртки, количество ядер в каждом слое, шаг сдвига ядра, необходимость субдискретизации, параметры полносвязной сети на выходе свёрточной и т.д. Все эти параметры выбираются исследователями эмпирически (через практику). Не хватает теоретических исследований, точных расчётов и рекомендаций для построения новых архитектур свёрточных ИНС.

Метод обратного распространения ошибки (backpropagation)

Метод обратного распространения ошибки (backpropagation) – это метод вычисления градиента, который используется при автоматическом обновлении весов многослойного перцептрона. Метод был исследован математиками в теории управления в начале 60-х годов двадцатого века, но впервые применён к ИНС лишь спустя 20 лет в 80-х годах. Метод является частным случаем более общей техники автоматического дифференцирования (automatic differentiation) и модификацией классического метода градиентного спуска (gradient descent).

Для метода обратного распространения ошибки прежде всего требуется построить функцию потерь или функцию оценки работы сети H. Простейшим и самым распространённым примером функции потерь является квадратичное отклонение:

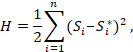(2.1)

где H – функция потерь; S_i – сигнал на i-том выходном нейроне ИНС; S_i^* – ожидаемый сигнал при правильном ответе на i-том выходном нейроне ИНС. Сумма берётся по всем выходным нейронам сети от 1 до n. Таким образом при квадратичном отклонении метод обратного распространения ошибки сводится к методу наименьших квадратов. Т.е. веса синапсов w_j,k,l и порог активации каждого нейрона C_j,k в ИНС должны быть такими, чтобы сумма (2.1) была минимальной, желательно, нулевой или близкой к нулю. Здесь j – номер нейронного слоя, k – номер нейрона в слое, l – номер связи в нейроне.

Метод наименьших квадратов не всегда является наилучшим выбором функции потерь. Умение конструировать оптимальную функцию потерь может существенно улучшить качество распознавания и на порядок ускорить обучение ИНС.

Теоретически можно подобрать оптимальные веса синапсов и порогов активации нейронов с помощью простого перебора, через прямое вычисление без применения эффективных приёмов (brute force computation). Однако на практике для многослойных глубоких сетей время такого прямого вычисления будет намного порядков превышать время жизни Вселенной.

Каждый синапс и каждый порог нейрона можно считать отдельным измерением некоего многомерного пространства. В глубокой ИНС таких синапсов и порогов тысячи, а иногда и десятки миллионов. При увеличении количества синапсов пространство становится многомерным и появляется проблема под названием «проклятие размерности», которая связанна с экспоненциальным возрастанием данных из-за увеличения размерности пространства. Например, чтобы покрыть единичный отрезок [0, 1] точками с частотой 0,01, требуется 100 точек. Чтобы покрыть квадрат с такой же частотой, требуется 10⁴ точек. Для десятимерного куба требуется уже 10^2*10=10²⁰ точек, что в 10¹⁸ раз больше, чем в одномерном пространстве. Таким образом использование переборных (brute force) алгоритмов становится неэффективным при возрастании размерности системы.

Ещё в 1961 году Ричард Беллман исследовал алгоритмы, которые хорошо работают в низких размерностях, но становятся неразрешимыми в высоких размерностях. Он назвал этот эффект «проклятие размерности». При увеличении размерности данные быстро становятся разреженными. Методы удаления избыточных и сильно скоррелированных данных позволяют уменьшить размерность. Одним из таких методов является метод обратного распространения ошибки.

Алгоритм обратного распространения ошибки состоит из пяти шагов.

Шаг 1. Конструируется функция потерь H, которая совсем не обязательно должна быть квадратичным отклонением (2.1).

Шаг 2. Высчитывается величина ошибки.

Шаг 3. Проверяется, достигла ли функция потерь минимума.

Шаг 4. Если функция потерь не достигла минимума, тогда параметры ИНС, т.е. веса синапсов и пороги активации, обновляются по итеративной формуле (2.2).

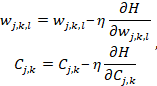(2.2)

где w_j,k,l – вес синапса; C_j,k – порог активации нейрона; H – функция потерь; 0 < η < 1 – множитель, задающий скорость обучения; j – номер нейронного слоя; k – номер нейрона в слое; l – номер связи в нейроне. Для обновления параметров ИНС нужно двигаться в обратном направлении от выходов ко входам сети и вычислять градиенты от функции потерь для каждого веса и порога. Обновлённые веса и пороги участвуют в обновлении следующих в обратном порядке слоёв ИНС.

Шаг 5. Повторять шаги 2–4 пока функция потерь не достигнет своего минимума. Когда функция потерь достигла минимума, ИНС считается обученной и готова к работе с новыми данными.

Величина шага коррекции ошибки задаётся с помощью множителя 0 < η < 1 (см. формулу 2.2). Шаг коррекции ошибки не должен быть слишком маленьким, иначе обучение будет долгим. Шаг коррекции ошибки не должен быть слишком большим, иначе можно «перешагнуть» через минимум, из-за чего в сети может возникнуть паралич (слишком большие веса) или неустойчивость (невозможность найти минимум функции потерь). Обычно множитель η не является константой и выбирается автоматически по следующему принципу: если градиент большой – множитель η маленький; если градиент маленький – множитель η большой.

При вычислении градиентов на шаге 4 алгоритма применяется цепное правило дифференцирования сложной функции (chain rule):

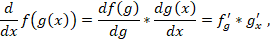(2.3)

где ƒ и g – функции переменной x.

Также применяется уравнение частной производной:

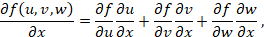(2.4)

где ƒ – функция трёх переменных u, v, w; и где x – четвёртая переменная, по которой производится дифференцирование.

К сожалению, пример с подробным вычислением минимума функции потерь не проводится в данной главе из-за её ограниченного объёма. Однако вы можете легко найти такие примеры в Интернете. Например, маленький и понятный курс видео лекций «Neural Networks Demystified» и соответствующие упражнения на GitHub.

Используя формулы (2.3) и (2.4) сначала корректируются веса и пороги для последнего нейронного слоя по формуле (2.2). Затем, используя скорректированные веса и пороги последнего слоя, корректируются веса и пороги предпоследнего слоя и т.д. Корректируются веса и пороги слоёв в обратном порядке, т.е. в направлении от выхода ко входу сети. При этом для коррекции следующего (в обратном порядке) слоя используются уже скорректированные параметры из предыдущих слоёв. Таким образом выполняется шаг 4 алгоритма.

При нахождении минимума функции потерь есть вероятность попасть в локальный минимум вместо глобального минимума. В этом случае применяются методы выхода из локальных минимумов.

При корректировке весов и порогов по формуле (2.2) градиент может стать слишком маленьким, что приведёт к замедлению или даже полной остановке обучения. До 2006 года проблема исчезающего градиента (the vanishing gradient problem) была основной причиной, из-за которой было невозможно обучать глубокие сети с множеством слоёв, потому что от слоя к слою градиент уменьшался при применении метода обратного распространения ошибки. Проблема исчезающего градиента вынуждала исследователей использовать неглубокие сети с небольшим количеством слоёв.

Проблема исчезающего градиента возникает из-за того, что градиент некоторого слоя является произведением градиентов всех предыдущих слоёв. Если градиенты на предыдущих слоях меньше единицы и лежат на отрезке [0, 1], тогда их произведение будет давать меньшее число. Например, 0,5*0,5=0,25, а при многократном умножении чисел, меньших единицы, их произведение будет стремиться к нулю и становиться исчезающе малым: 0,5¹⁰ ≈ 0,00098.

В 2006 году вышли три статьи Яна Лекуна (Yann LeCun), Джошуа Бенджио (Yoshua Bengio) и Джеффри Хинтона (Geoffrey Hinton), в которых они предложили новую архитектуру ИНС, способную преодолеть проблему исчезающего градиента: глубокую сеть доверия (deep belief network), которая может быть представлена, как последовательность автокодировщиков под названием ограниченные машины Больцмана (restricted Boltzmann machine). Сейчас глубокая сеть доверия не является единственной архитектурой и техникой для преодоления проблемы исчезающего градиента, но в то время глубокие сети доверия произвели революцию в ИНС. Например, выбор активационной функции ReLU позволяет частично устранить эту проблему. На данный момент самой популярной архитектурой ИНС для преодоления проблемы исчезающего градиента является глубокая остаточная нейронная сеть (Residual Network, ResNet). Преодоление проблемы исчезающего градиента привело к повышению интереса к ИНС и развитию глубокого обучения (Deep Learning).

Кроме проблемы исчезающего градиента существует проблема взрывного градиента, которая является обратной к исчезающему, но результат у них один – прекращение обучения. В глубоких и/или рекуррентных ИНС градиенты ошибок могут накапливаться во время обновления, в результате чего градиент может становиться очень большим. Большие градиенты приводят к нестабильной работе сети. Если вес синапса станет слишком большим из-за больших обновлений, то это приведёт к параличу сети. Также большой вес может привести к численному переполнению, выходу за пределы максимально возможного числа для компьютерной программы. Известно, что полезная информация хранится в весах синапсов, а не в состояниях нейронов. Поэтому, если разница между весами становится слишком маленькой, то в системе начинают доминировать шумы. Если разница между весами становится слишком большой, то эта синаптическая связь начинает подавлять другие связи.

Градиенты в глубоких ИНС являются нестабильными и стремятся либо к нулю, либо к бесконечности при продвижении к первым слоям многослойной сети. Эта нестабильность является фундаментальной проблемой для методов обучения глубоких ИНС с помощью градиентов.

Переобучение и недообучение

Переобучение (overfitting) – явление, при котором ошибка модели на объектах, не участвовавших в обучении, оказывается существенно выше, чем ошибка на объектах, участвовавших в обучении. Переобучение возникает при использовании слишком сложных моделей, как правило, с большим количеством нейронов и синапсов, либо при слишком долгом процессе обучения, либо при неудачной обучающей выборке.

Недообучение (underfitting) – явление, при котором ошибка обученной модели оказывается слишком большой. Недообучение возникает при использовании слишком простых моделей, как правило, с малым количеством нейронов и синапсов, либо при прекращении процесса обучения до достижения состояния с достаточно малой ошибкой, либо при неудачной обучающей выборке.

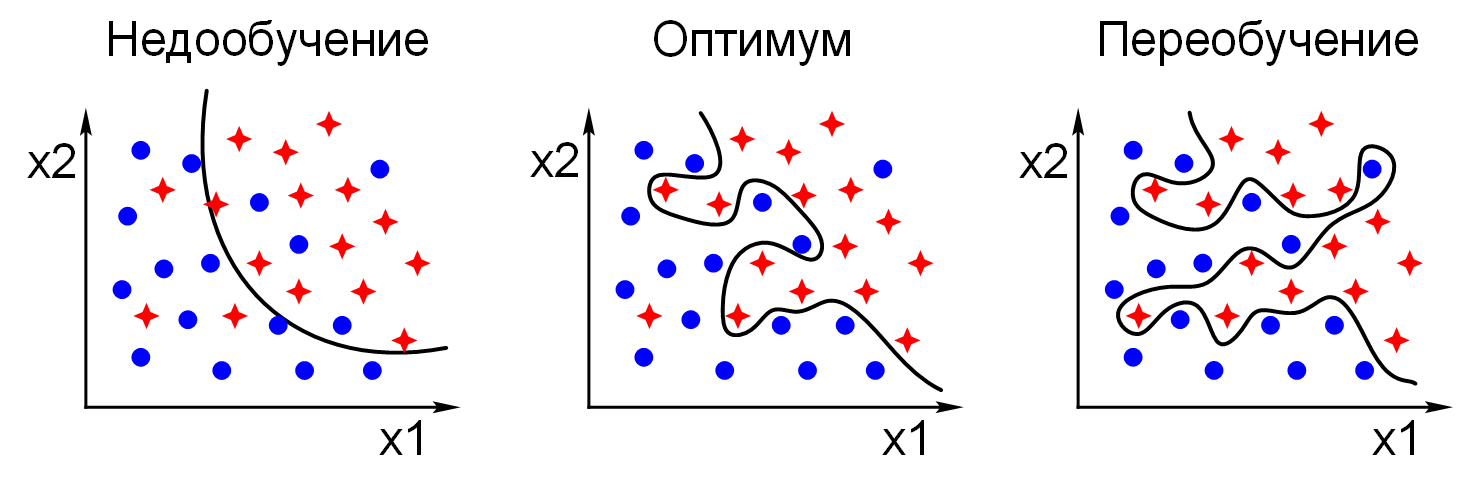
На рисунке 2.5 приведены примеры недообученной, обученной и переобученной модели в задаче классификации.

Рис. 2.5 – Недообучение, оптимум и переобучение в классификации

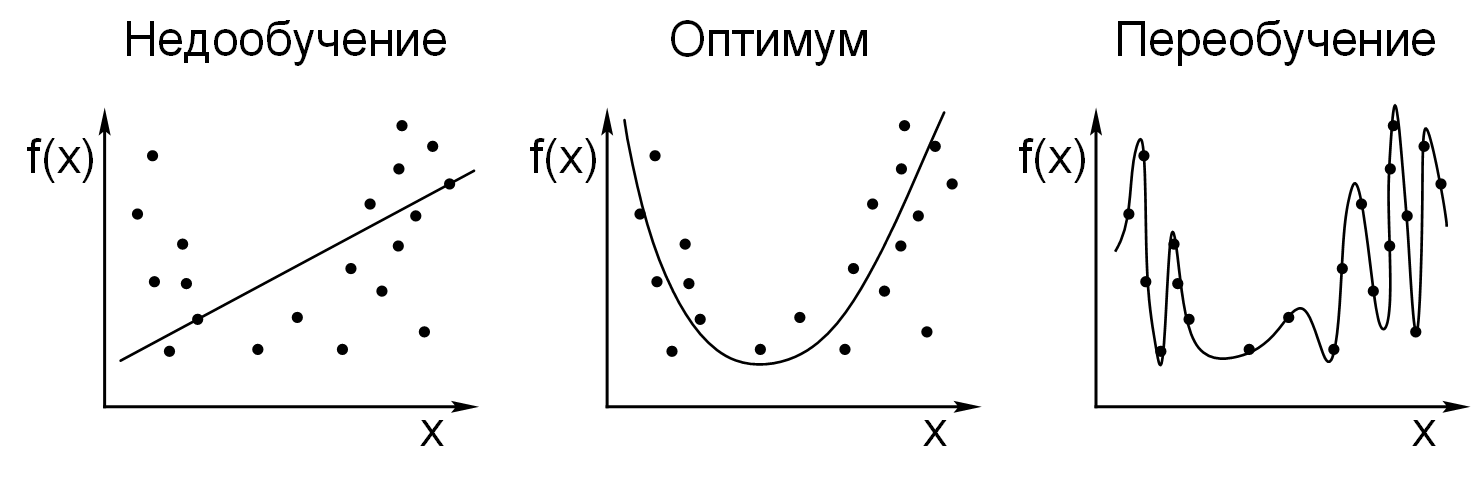
На рисунке 2.6 приведены примеры недообученной, обученной и переобученной модели в задаче регрессии.

Рис. 2.6 – Недообучение, оптимум и переобучение в регрессии

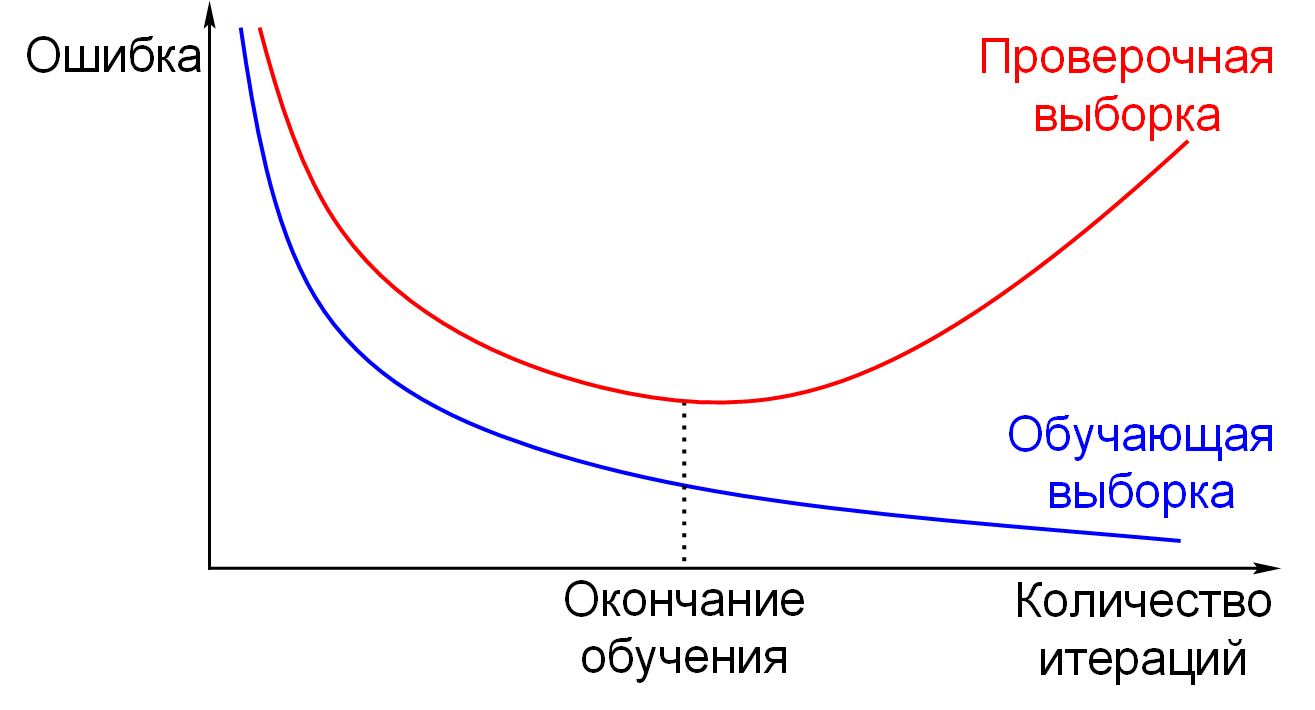
Причины переобучения разнообразные:

• слишком мало данных для обучения либо слишком много нейронов и синапсов в ИНС – модель запомнила все варианты из обучающей выборки и, таким образом, утратила возможность обобщения, выдавая запомненные варианты вместо предсказаний;
• слишком долгое обучение – модель находит закономерности в шуме (галлюцинирует);
• плохо подготовленные данные в обучающей выборке могут привести к тому, что модель будет давать большую ошибку на новых данных, которые не участвовали в обучении.

Если модель запомнила все варианты в обучающей выборке, то новые примеры она может не угадать просто потому, что они отличаются от тех, что были в выборке. Эта проблема возникает, когда обучающая выборка слишком маленькая либо модель ИНС слишком сложная.

Если модель находит закономерности в шуме, то новые данные будут обладать другим шумом, который всегда есть в данных, тогда ответ модели будет ошибочным. Эта проблема возникает, когда обучение было слишком долгим и модель просто подогнана под шум в обучающей выборке (рисунок 2.7).

Рис. 2.7 – Окончание обучения, дальше модель переобучается

Для того, чтобы контролировать модель на переобучение, нужно использовать отдельные наборы данных для обучения и оценки. Данные, на которых происходит оценка качества, не должны участвовать в обучении.

Рекомендации по созданию обучающей выборки

Важность правильной подготовки данных

Важность правильной подготовки данных для алгоритмов машинного обучения трудно переоценить: примерно 80% времени тратится на работу с данными и менее 20% – на создание модели. Плохо подготовленные данные дадут плохие результаты или результатов не будет.

У специалистов по работе с данными есть принцип «Мусор на входе – мусор на выходе» (Garbage In, Garbage Out), который означает, что при плохих входящих данных будут получены плохие результаты, даже если сам алгоритм правильный. Качество данных – это многоаспектное понятие. Данные должны быть: точными, непротиворечивыми, полными, достоверными, объективными, актуальными, репрезентативными и др. Провал в каком-либо из аспектов качества может сделать данные малопригодными или бесполезными. Самое худшее, если данные выглядят пригодными, но ведут к ложным результатам.

Разберём несколько ошибок при создании обучающей выборки.

Предположим, что в городе Минск есть поликлиника, где граждане каждый год проходят флюорографию. Для простоты мысленного эксперимента будем считать, что городская поликлиника только одна. Кроме поликлиники «для всех» в посёлке Боровляны около Минска есть онкологический центр, куда направляются граждане с подозрением на раковые заболевания. В городской поликлинике есть бюджетный цифровой флюорограф, а для онкоцентра был куплен дорогой цифровой флюорограф последней модели, потому что люди с подозрением на рак должны обследоваться тщательнее. Все флюорограммы грудной клетки из поликлиники и онкоцентра сохраняются в единую базу данных медицинских снимков. Перед исследователем стоит задача: используя нейронные сети, научиться определять здоров человек или нет по флюорограмме его лёгких.

Первая ошибка: взять все флюорограммы из базы данных и подать их на вход нейронной сети в качестве обучающей выборки. Ошибка в том, что подавляющее большинство людей в обучающей выборке будут здоровы, поэтому для достижения высокой точности правильных ответов достаточно всегда выдавать один и тот же ответ «здоров». Предположим, из 10 000 человек только 10 будут больны. Значит количество больных составляет: (10/10 000)*100% = 0,1%, а количество здоровых равно: 100% ‒ 0,1% = 99,9%. Если всегда выдавать ответ «здоров», то точность правильных ответов составит 99,9%, а ошибка такого «предсказания» окажется очень маленькой: всего одна ошибка на тысячу правильных ответов или 0,1%.

ИНС тренируется по принципу «чем больше правильных ответов, тем лучше», но для людей необходимо выявлять больных людей, а не считать правильные ответы.

Математически это можно выразить через статистические показатели эффективности теста бинарной классификации – чувствительность и специфичность:

(2.5)

Чувствительность (true positive rate, TPR) равна доле правильно идентифицированных положительных результатов, т.е. вероятности того, что больной будет классифицирован как больной. Специфичность (true negative rate, SPC) равна доле правильно идентифицированных отрицательных результатов, т.е. вероятности того, что здоровый будет классифицирован как здоровый. Здесь «положительный результат» – это синоним болезни, а «отрицательный результат» – это синоним здоровья. Такие термины приняты в медицинской практике.

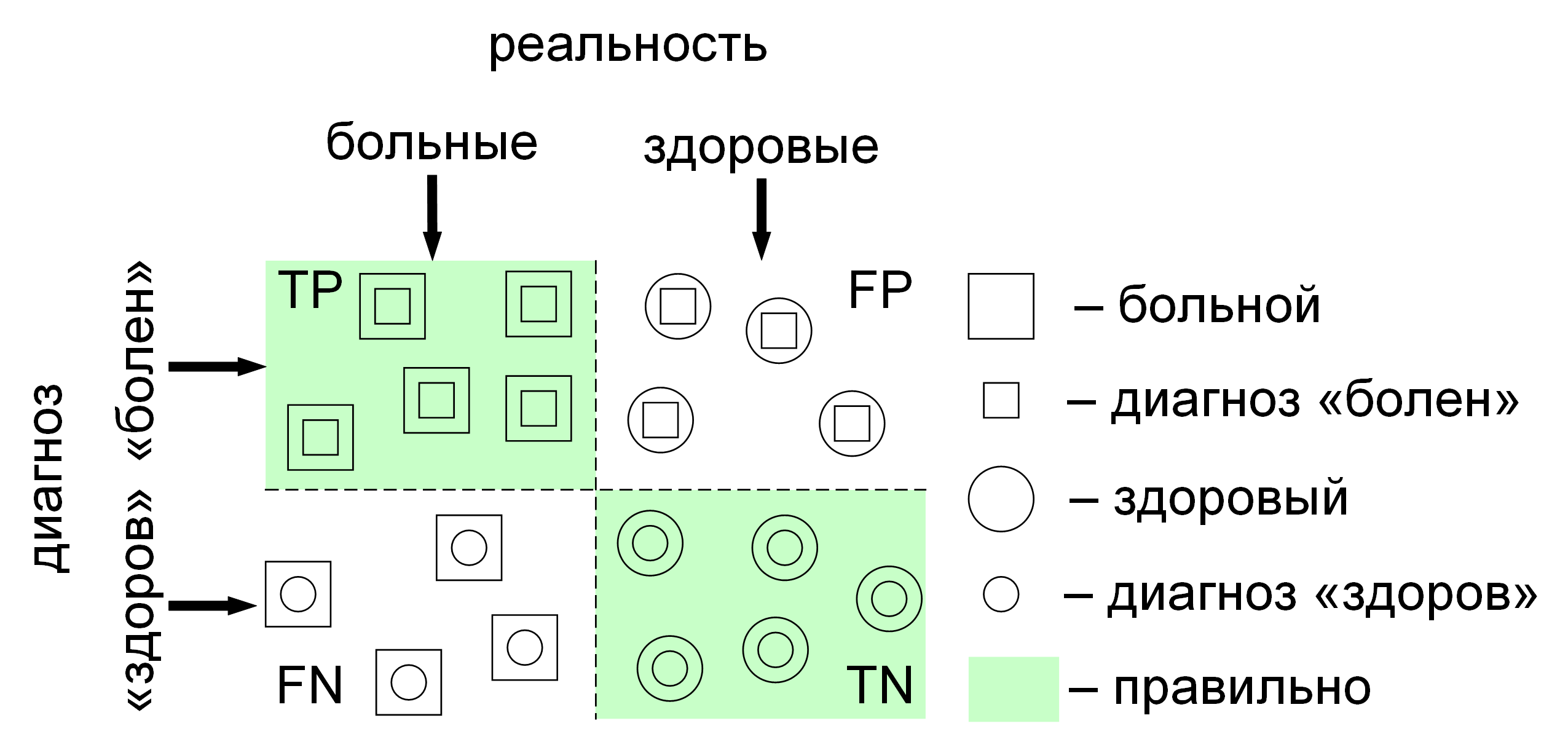
Бинарный классификатор разделяет всё множество (людей) на два класса: больные и здоровые. Всего есть четыре типа ответов бинарного классификатора (рисунок 2.8):

1. Истинно положительный (true positive, TP): больные правильно идентифицируются как больные.
2. Ложно положительный (false positive, FP): здоровые неверно идентифицируются как больные.
3. Ложно отрицательный (false negative, FN): больные неверно идентифицируются как здоровые.
4. Истинно отрицательный (true negative, TN): здоровые правильно идентифицируются как здоровые.

Рис. 2.8 – Четыре вида ответов бинарного классификатора:
TP – true positive (правильно);
TN – true negative (правильно);
FP – false positive (ошибка первого рода);
FN – false negative (ошибка второго рода).

Когда классификатор всегда выдаёт ответ «здоров», то, в соответствии с формулой (2.5), его чувствительность равна нулю, а специфичность равна единице:

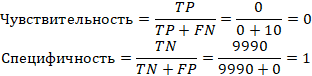(2.6)

Для того, чтобы исправить ошибку с несбалансированными данными, нужно сбалансировать обучающую выборку по больным и здоровым, т.е. взять одинаковое количество больных и здоровых. Например, десять тысяч флюорограмм здоровых людей должны «уравновешиваться» каким же количеством флюорограмм больных людей, иначе обучающая выборка будет несбалансированной и получится вышеописанная ошибка обучения.

Вторая ошибка: взяли 10 000 флюорограмм здоровых людей и 10 000 флюорограмм больных людей из общей базы и подали их на вход ИНС в качестве обучающей выборки. Ошибка в том, что здесь не учтено равновесие обучающей выборки по моделям цифровых флюорографов. Очевидно, что каждая модель и даже каждый отдельный экземпляр одной и той же модели делает различные снимки. Снимки различаются оттенками, цветовой гаммой, резкостью, градиентами и даже тем, что у одного флюорографа подставочка будет немного выше, чем у другого, из-за чего снимки грудных клеток в онкоцентре будут чуть выше, чем снимки грудных клеток в поликлинике.

В условии задачи сказано, что в онкоцентр направляются люди с подозрением на заболевание, там их тщательно обследуют, делают множество снимков их грудной клетки. Как результат, в базе данных будет преобладающее количество снимков больных из онкоцентра, которое будет превышать количество снимков больных из поликлиники в разы. Также соотношение между снимками больных и здоровых в онкоцентре будет гораздо выше, чем соотношение между снимками больных и здоровых в поликлинике, потому что больных в онкоцентре больше.

Допустим, снимки из онкоцентра имеют синеватый оттенок по сравнению со снимками из поликлиники. Таким образом нейронная сеть вместо определения реальных больных будет искать синеву на снимках, потому что большинство снимков больных были сделаны в онкоцентре. Если снимок имеет синеву – это больной, а если не имеет синевы – это здоровый. В результате на выходе ИНС будут высокие показатели правильных ответов, а исследователь не будет знать, что допустил ошибку, пока не опробует свою обученную модель на третьей модели флюорографа и увидит, как резко упала точность классификации.

Конечно, можно нормировать все снимки по цвету, но оттенок – это только одно из многих различий между изображениями с разных моделей приборов. Самым лучшим решением будет уравновесить снимки по различным моделям цифровых флюорографов. Например, взять 5 000 флюорограмм больных и 5 000 флюорограмм здоровых из онкоцентра, затем взять 5 000 флюорограмм больных и 5 000 флюорограмм здоровых из поликлиники. Таким образом обучающая выборка станет сбалансированной по различным моделям флюорографов. После этого желательно ещё и нормировать все отобранные снимки по цвету, резкости, отцентрировать их и т.д.

Внимательно и осознанно выбирайте метрику под ваш набор данных. В случае сильно несбалансированных признаков можно получить бесполезную метрику.

Аугментация данных (data augmentation)

Аугментация данных (data augmentation) – это методика создания дополнительных обучающих данных из имеющихся данных. Целей у аугментации несколько:

1. «раздуть» обучающую выборку;
2. повысить точность работы нейронной сети и её устойчивость к шумам;
3. облегчить работу по созданию базы данных для обучения.

Для обучения глубокой ИНС нужно много данных: десятки и сотни тысяч изображений. Не всегда получается найти достаточное количество данных. На многие изображения распространяются лицензионные соглашения их обладателей, а также право на неприкосновенность частной жизни, врачебная тайна для медицинских изображений и т.д. Базы данных часто являются платными, потому что проделана огромная работа для создания таких баз. Если вы станете фотографировать людей и/или их собственность на улице, то это может вызвать обоснованные претензии и даже агрессию. В уголовных кодексах разных стран предусмотрена ответственность за «незаконные собирание либо распространение информации о частной жизни». Генерация искусственных изображений позволяет избежать проблем с законом и получить множество изображений бесплатно.

Создание дополнительных изображений с различными искажениями позволяет повысить точность работы нейронной сети и её устойчивость к шумам. Например, повороты позволят получать правильные ответы даже если изображение повёрнуто на некоторый угол.

Чтобы создать хорошую базу данных изображений, их нужно: собрать, обработать (кадрировать, фильтровать и т.д.), разметить (выделить области интереса, regions of interest, ROI, и присвоить им метку, название объекта на изображении). К тому же требуется собрать разнообразные данные и сбалансировать их по различным моделям фотокамер, при различном освещении, с различных ракурсов и т.д. Эти операции требуют значительных затрат рабочего времени, которые можно уменьшить путём аугментации данных.

Для аугментации берутся несколько шаблонов, «идеальных» примеров, и с помощью различных искажений создаются дополнительные примеры для обучения. Можно сгенерировать новые изображения с использованием естественных. Применяются следующие искажения и их различные комбинации:

• геометрические (повороты, сдвиги, растяжения, сжатия, зеркальные отражения, случайное кадрирование, random crop, афинные, проективные и т.д.);
• яркостные и цветовые (изменения яркости, цветовой гаммы, color jitter, изменения тона, насыщенности и значения цветового пространства HSV и т.д.);
• замена фона;
• характерные искажения для решаемой задачи (шумы, блики, дополнительные линии, размытие, разфокусировка и т.д.).

Генерировать изображения можно с помощью библиотек для работы с изображениями или специальных программ. Наилучший результат получается, если комбинировать естественные (реальные) и искусственные (сгенерированные) изображения, например, аугментировать естественные изображения.

Отбор признаков (feature selection)

Каждый объект характеризуется набором признаков (features, «фичей», параметров). Например, объект «сообщение электронной почты» характеризуется следующим набором признаков: набор слов, длина сообщения, дата, отправитель, получатель, язык, частота сообщений от данного адресата и т.д. Признаком объекта (изображения, текста, звука) может быть любая количественная характеристика, главное, чтобы эта характеристика была уникальной именно для данного типа объектов: расположение особых точек на изображении, вычисляемых через алгоритм SURF; спектр сигнала; гистограмма; частота встречаемости пар точек на изображении; градиенты (перепады) яркости на изображении и т.д.

Чем больше признаков, тем дольше работа алгоритма. Это очевидно.

На первый взгляд кажется, чем больше признаков, тем больше полезной информации в результате получится. Это неочевидно, но далеко не всегда увеличение количества признаков даёт положительные результаты. Например, если при составлении прогноза продаж, учитывать в качестве дополнительного параметра фазу Луны, то предсказание только ухудшится. Поэтому прогнозы улучшают, отбрасывая ненужные признаки и оставляя нужные, проводят отбор признаков.

Отбор признаков (feature selection) требует от исследователя интуиции, хорошего знания предмета изучения, умения отделять главное от второстепенного. Отбор признаков для изображений заключается в их предварительной обработке: увеличение контрастности, отсекание фона, подавление шумов и т.д. Отбор признаков помогает решить следующие задачи:

• упростить модель с целью лучшего понимания её работы;
• уменьшить время обучения;
• избежать «проклятия размерности»;
• сократить переобучение.

Стоит отличать отбор признаков (feature selection) от извлечения признаков (feature extraction). Отбор признаков – это выбор подмножества признаков из имеющихся без преобразования объекта, например, изображение остаётся изображением. Извлечение признаков – это преобразование объекта, т.е. преобразование отобранных признаков в пространство более низкой размерности. Например, при извлечении признаков изображение преобразуется в вектор признаков и фактически перестаёт быть изображением. При преобразовании объекта, при извлечении признаков, такие измеряемые величины, как длина, время, вес, цвет, как правило, теряются. Извлечение признаков трансформирует набор первоначально отобранных признаков в другой набор, более подходящий для машинного обучения.

Хотя отбор признаков формально является частным случаем извлечения признаков, для отбора признаков применяются собственные уникальные алгоритмы и методы. Техники отбора признаков можно разделить на три категории: обёртки (wrapper methods), фильтры (filter methods) и встроенные методы (embedded methods). Также автоматический отбор признаков заложен в таких ИНС, как автокодировщики.

Часто применяют цепочки методов машинного обучения, когда признаки, полученные с выхода предыдущего метода, подаются на вход следующего метода.

Самая распространённая ошибка – это провести отбор признаков у всей базы данных до обучения. Отбор признаков – это неотъемлемая часть процесса обучения, поэтому нужно делать отбор признаков независимо для обучающей и для проверочной выборок. Если этого не сделать и провести отбор признаков у всей базы данных, то в данные непреднамеренно будет внесено искажение, что приведёт к переобучению. Например, если сделать отбор признаков до проведения k-кратной перекрёстной проверки (смотрите следующий раздел «Обучение модели»), тогда информация из проверочной (validation) и из тестовой (test) выборок будет использована при обучении в обучающей (train) выборке.

В этом случае проверочная и тестовая выборки будут участвовать в отборе признаков для обучающей выборки, а обучающая выборка будет участвовать в отборе признаков для проверочной и тестовой выборок. Но проверочная, тестовая и обучающая выборки должны быть независимыми, иначе данные станут искажёнными. Значит отбор признаков должен проводиться независимо для обучающей и проверочной выборок на каждой итерации k-кратной перекрёстной проверки, а также независимо для обучающей и тестовой выборок на этапе разделения данных на две части. Например, такой признак, как отклонение от средней площади квартиры, должен определяться независимо для обучающей, проверочной и тестовой выборок, а не для всей базы данных квартир целиком.

Извлечение признаков (feature extraction)

Извлечение признаков связано с уменьшением размерности пространства признаков.

Признаки могут быть извлечены из данных «как есть»: вес, рост, возраст, число покупок, RGB пиксели на изображении и т.д.

Признаки могут быть спроектированы исходя из опыта и интуиции. Например, уход клиента может быть связан с количеством обращений в техподдержку, значит, можно выделить признак «число обращений в техподдержку».

Признаки могут быть извлечены автоматически с помощью интеллектуального анализа данных (data mining). Часто автоматически извлечённые признаки бывают лучше, чем разработанные вручную.

Для сложных объектов уже есть готовые «классические» техники извлечения признаков: SVM, SIFT, HoG, преобразование Хафа, PCA, MFCC и т.д.

ИНС умеют автоматически извлекать признаки. Результатом работы свёрточной ИНС является вектор признаков (descriptor, «дескриптор»), который представляет собой набор чисел, характерный для данного класса объектов. Найденные вектора признаков подаются на классификатор для разбиения их на классы. Классификатором часто является другая ИНС, например, полносвязные слои нейронов (fully connected layers), а также любые алгоритмы классификации, например, SVM, k-NN, логистическая регрессия, наивный байесовский классификатор и т.д.

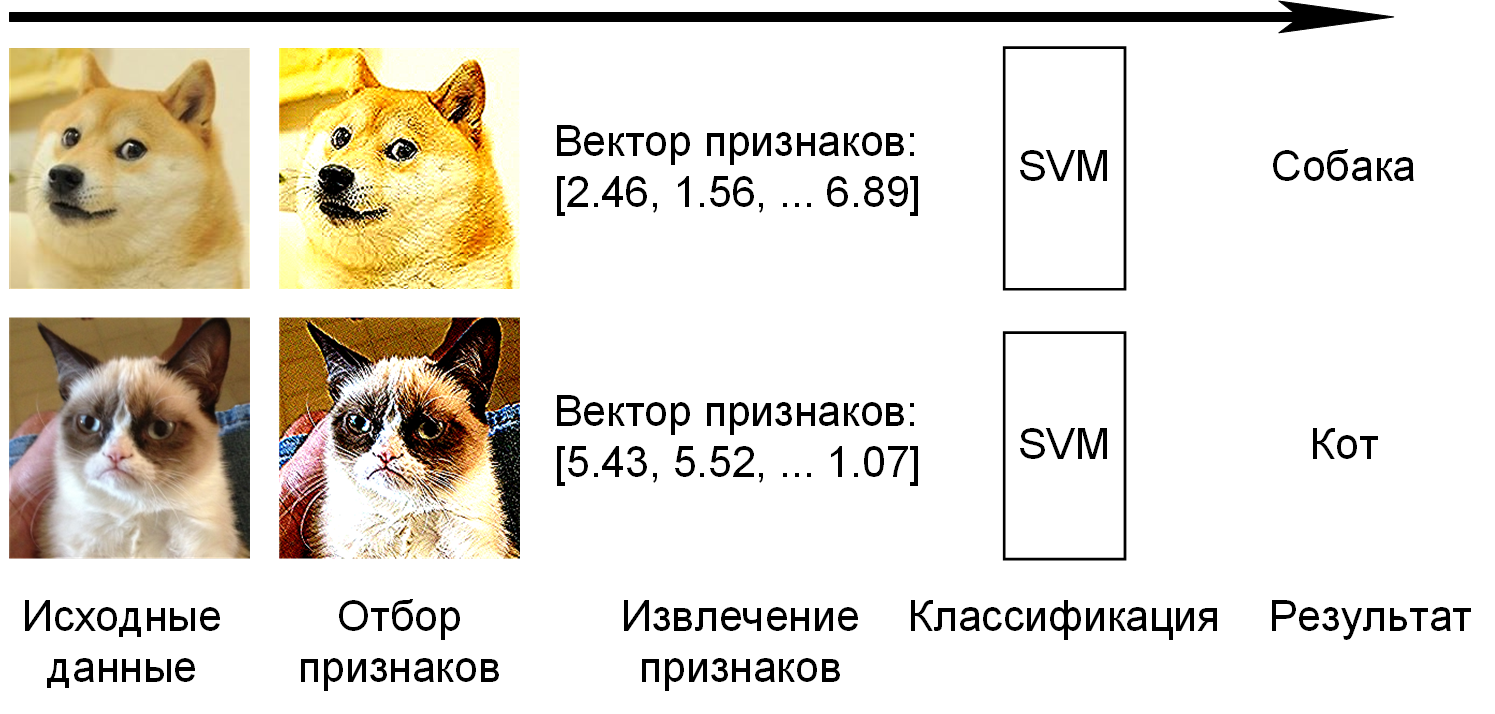
Процесс отбора и извлечения признаков для изображений представлен на рисунке 2.9:

Рис. 2.9 – Отбор и извлечение признаков

Проектирование признаков (feature engineering)

Существует множество техник, которые позволяют заметно увеличить качество разрабатываемых алгоритмов. Одна из таких техник – это проектирование (создание, разработка) признаков (feature engineering). В то время, как методы отбора признаков хорошо изучены и уже существует большое количество алгоритмов для этого, задача создания признаков является своего рода искусством и часто является самым сложным этапом машинного обучения.

Например, с помощью линейной регрессии можно прогнозировать цену дома, как линейную комбинацию длины и ширины дома. Но цена дома в первую очередь зависит от его площади, которая никак не выражается через линейную комбинацию длины и ширины. Качество алгоритма увеличится, если длину и ширину заменить на их произведение. Тем самым получается новый признак, который заметно влияет на цену, а пространство признаков сокращается: вместо двух признаков длины и ширины теперь один признак – площадь.

Сложно придумать метод, который для любой задачи давал бы технику построения признаков. Автоматизация построения признаков стала новой темой исследований. Например, Deep Feature Synthesis алгоритм по автоматическому построению признаков от исследователей Массачусетского технологического института, который распространяется как библиотека с открытым исходным кодом под названием Featuretools.

В качестве признака можно взять результат работы других алгоритмов. Например, при решении задачи классификации можно сначала решить задачу кластеризации и в качестве признака взять кластер объекта.

Оценка потенциальной пригодности признаков (созданных или отобранных) проводится последовательным независимым тестированием каждого признака с помощью t-теста или z-теста, где определяется статистическая значимость признака. Данная оценка может быть выполнена с помощью программного обеспечения Statistica или на языках программирования R, Python, Delphi, C++ и т.д. с дополнительными библиотеками статистического анализа. Следует помнить, что корректность t-теста обеспечивается только в случае Гауссовского распределения значений признака. Поэтому желательно провести предварительный тест на нормальность распределения значений признака.

Наглядным способом оценки информативности признаков является визуализация объектов (изображений) как точек в N-мерном пространстве признаков путём редуцирования размерности до двух методом многомерного масштабирования (Multi-Dimensional Scaling, MDS) с последующим анализом получаемых диаграмм рассеяния (scatterplots) при варьировании признаков. Визуализация позволяет оценить степень пересечения классов, идентифицировать резко выделяющиеся объекты, сделать предварительную оценку и т.д.

Другое семейство способов отбора основано на непосредственном использовании признаков для классификации объектов и вычисления важности (веса) каждого признака с точки зрения степени полезности для классификации (метод случайных лесов, генетические алгоритмы, ИНС и др.).

Желательно, чтобы набор признаков был взаимно не коррелируемым, т.е. чтобы признаки не зависели друг от друга.

Часто, чтобы эффективно решить задачу, необходимо быть экспертом в этой области и понимать, какие параметры влияют на конкретную целевую переменную. Каждый знает, что цена квартиры зависит в первую очередь от площади, однако в других предметных областях такие заключения делать достаточно сложно.

Также стоит помнить теоремы об отсутствии бесплатных обедов: «No free lunch theorems». Смысл этих двух математических теорем в том, что не существует алгоритма поиска, алгоритма оптимизации или алгоритма обучения с учителем, который «работает» лучше других на всём множестве задач. Если некоторый алгоритм работает лучше (быстрее, точнее) на одних задачах, значит, на других задачах он будет хуже. Т.е. способ решения задачи неотделим от данных, применяемых в этой задаче.

Преобразования признаков (feature transformations)

В машинном обучении существует большое количество преобразований признаков: монотонное преобразование, изменение распределения, центрирование, регуляризация, выделение главных компонент, объединение (bundling), дискретизация, масштабирование, нормализация и т.д. [2.13]. Примеры преобразования признаков изображены на рисунке 2.10.

Рис. 2.10 – Примеры преобразования признаков

Целей у преобразований признаков много и все они разные для разных преобразований: исследование данных, подготовка данных для конкретного метода машинного обучения, устойчивость к шумам и выбросам, создание новых признаков, повышение точности и т.д.

Монотонное преобразование признаков критично для одних алгоритмов и не оказывает влияния на другие. Нечувствительность к монотонному преобразованию признаков является одной из причин популярности деревьев решений (decision trees) и всех производных алгоритмов (случайный лес, градиентный бустинг и т.д.), потому что не все исследователи умеют и хотят работать с преобразованиями признаков, а алгоритмы на основе деревьев решений устойчивы к необычным распределениям.

Например, нужно предсказать стоимость квартиры по двум признакам – удалённости от центра и количеству комнат. Количество комнат редко превосходит 5, а расстояние от центра в больших городах измеряется десятками тысяч метров. В результате метод ближайших соседей (kNN) не будет работать, потому что квартиры не будут группироваться по комнатам, а только по расстоянию до центра города. В этом случае необходимо использовать одну и ту же метрику, т.е. преобразовать метры и комнаты в безразмерные величины с одной и той же плотностью распределения значений. Но это не всегда возможно, так как по некоторым метрикам нельзя или трудно провести оптимизацию (AUC, NDCG).

ИНС получили такую большую популярность, потому что они проектируют, извлекают и преобразуют признаки автоматически. Однако нужно помнить про правило «Мусор на входе – мусор на выходе», когда даже самая лучшая ИНС не сможет работать с плохо подготовленными данными.

Обучение модели

Разбиение данных для обучения и оценки

Когда данные подготовлены, они разбиваются случайным образом на две части: для обучения (обучающая выборка, train set) и для оценки качества (тестовая выборка, test set). Данные для оценки качества не участвуют в обучении. Это необходимо по двум причинам.

Во-первых, если оценивать качество на той же выборке, на которой обучалась модель, то результаты всегда будут завышенными. При использовании обученной модели на реальных данных её точность снизится. Чтобы узнать насколько снизится точность на реальных данных, используются данные для тестирования, которые не участвовали в обучении.

Во-вторых, модель может переобучиться и, чтобы вовремя заметить переобучение, периодически проводят оценку качества на данных для тестирования, которые не участвуют в обучении.

Метод разбиения данных на обучающую и тестовую выборки называется методом удержания (holdout method).

Как правило, данных для обучения ИНС не бывает слишком много. Не помогает даже «раздутие» данных с помощью аугментации. Часто не хватает нужных данных в каком-либо классе. Например, количество здоровых обычно значительно превышает количество больных. На сегодня задача сокращения данных для качественного обучения является главной проблемой развития ИНС.

Чтобы увеличить обучающую выборку применяют способ, который называется k-кратная перекрёстная проверка (k-fold cross-validation, «кросс-валидация», метод перекрёстного или скользящего контроля), который состоит из четырёх шагов.

1. Исходная обучающая выборка случайным образом разбивается на k непересекающихся (разных) примерно равных по размеру частей.
   
2. (k-1) частей применяются для обучения, а оставшаяся одна часть используется для проверки (валидации или контроля). Данная процедура повторяется k раз, т.е. происходит k итераций. Таким образом все данные для обучения используются в проверке. На практике чаще всего выбирается k = 10, т.е. модель обучается на 9/10 данных и проверяется на 1/10.
   
3. После k итераций строятся k моделей и соответственно k оценок для ошибки предсказания.
   
4. В качестве окончательной оценки ошибки берётся их среднее взвешенное значение.
   

Когда одна k-кратная перекрёстная проверка завершена, то говорят, что пройдена одна эпоха. Эпох может быть много. Для этого данные снова случайным образом разбиваются на k частей, и перекрёстная проверка повторяется (рисунок 2.11).

Рис. 2.11 – Разбиение данных при обучении:
метод удержания и методы k-кратной перекрёстной проверки (эпохи)

Проверку на переобучение с помощью тестовой выборки желательно совершать после каждой эпохи. Частным случаем метода перекрёстной проверки является метод перекрёстной проверки с одним отделяемым элементом (leave-one-out cross-validation, LOOCV), при котором величина проверочной выборки равна одному элементу. Метод с одним отделяемым элементом является самым точным, но требует много времени и компьютерных ресурсов.

Кроме методов удержания и k-кратной перекрёстной проверки существует множество методов повторного взятия выборки (resampling methods), рассмотрение которых выходит за рамки этой главы. Однако цель всех этих методов одна – увеличить объём данных для обучения, не ухудшая качества обучения.

Будьте внимательны: отбор, извлечение и преобразование признаков для обучающей, проверочной и тестовой выборок должны быть независимыми. Например, нахождение среднего роста для обучающей выборки должно быть независимым от нахождения среднего роста для проверочной выборки. Если находить средний рост по всем данным и использовать его в преобразовании параметров, а потом уже разделять данные на обучающую и проверочную выборки, то информация из проверочной выборки будет участвовать в обучении, и, таким образом, результаты обучения будут искажены.

Процесс обучения

Обучение происходит на тренировочных данных (train set). Обучение может означать подстройку каких-то численных параметров модели без изменения её структуры (чаще) или изменение структуры самой модели (реже).

Во всех ИНС есть гиперпараметры – это значения, которые нужно подбирать вручную, эмпирически, методом проб и ошибок. На данный момент никто не может дать точный математический ответ для всевозможных задач машинного обучения:

• сколько данных нужно для обучающей выборки;
  
• сколько времени будет проходить обучение;
  
• на сколько частей разбивать тренировочную выборку;
  
• оптимальное количество скрытых слоёв;
  
• количество нейронов в каждом слое;
  
• количество синапсов в каждом нейроне;
  
• размер ядер свёртки и шаг свёртки для свёрточных ИНС;
  
• какую метрику взять для оценки качества обучения и т.д.;
  

потому что не существует теории и математического аппарата для вычисления точных значений гиперпараметров. Существуют лишь общие рекомендации, например, не стоит делать ИНС с 1000 нейронов для решения простых задач. Обычно для достижения успеха требуется испытать разные варианты одной модели или даже модели различных типов. Экспериментируйте!

Как правило, подобранные значения гиперпараметров не меняются во время обучения и использования ИНС. Каждая архитектура ИНС имеет свой уникальный набор гиперпараметров, который требуется подобрать и настроить вручную, если требуется сделать новую ИНС. Чем больше гиперпараметров, тем труднее настроить ИНС.

Оценка качества обучения

Оценка качества является прикладной задачей анализа данных. Точность и качество работы алгоритма в машинном обучении измеряется метрикой качества. Метрика – это правило определения расстояния между любыми двумя точками. Каждый объект может быть представлен, как точка в некотором многомерном (метрическом) пространстве. В общем, основная задача машинного обучения как раз и заключается в представлении объектов в виде точек в многомерном пространстве и определении метрики, т.е. расстояния между этими точками.

Разные задачи подразумевают различные метрики качества. Условно выделяют четыре класса метрик, которые применяются в машинном обучении и на практике редко соответствуют друг другу: бизнес-метрики, онлайн-метрики, офлайн-метрики, метрики обучения ИНС. Желательно использовать одну и ту же метрику для обучения и оценки качества, но это не всегда возможно.

Бизнес-метрики важны для рынка, финансового планирования, построения бизнес-модели и направлены на измерение доходов и потерь: ключевые показатели эффективности (key performance indicators, KPI), лояльность и удержание клиентов, стоимость получения клиента, скорость оттока клиентов, коэффициенты производительности и т.д.

Онлайн-метрики доступны в работающей системе в реальном времени. Например, среднее время просмотра сайта пользователем, количество просмотров страницы, самые популярные товары в данный момент, котировки акций на бирже, курсы валют, поисковые запросы и т.д.

Офлайн-метрики – это метрики, которые можно посчитать на исторических данных, т.е. данных, которые были измерены в прошлом и хранятся отдельно от работающей системы в логах, записях, базах данных и т.д.: среднеквадратичное отклонение (root-mean-square error, RMSE), среднее абсолютное отклонение (mean absolute error, MAE), средняя абсолютная процентная погрешность (MAPE), средняя процентная ошибка (MPE), коэффициент детерминации (R², R-квадрат) и т.д. К офлайн-метрикам также относятся различные метрики качества бинарной классификации: чувствительность, специфичность (см. формулу 2.5), аккуратность (accuracy), площадь под ROC-кривой (ROC AUC), F-мера (представляет собой гармоническое среднее между точностью и полнотой) и др.

Метрики обучения ИНС – это различные функции потерь искусственных нейронных сетей: логарифмическая потеря (Log Loss, Cross Entropy Loss), минимакс (MinMax Rule), ошибка перекрестной проверки (CV error), матрицы неточностей и т.д. В случае многоклассовой классификации обычно применяется категорийная кросс-энтропия (categorical cross-entropy).

Выбросы (аномальные значения) могут сильно исказить метрику. Поэтому желательно использовать устойчивую к выбросам метрику либо отсеивать выбросы. Например, медиана устойчивее к выбросам, чем арифметическое среднее. Более того, каждый сигнал имеет в себе шум даже самый «чистый». Одним из критериев хорошего алгоритма является его устойчивость к шумам. Регуляризация (regularization) – это один из способов сделать алгоритм устойчивым к шумам и выбросам.

Регуляризация является основным методом из категории встроенных методов (embedded methods) отбора признаков (смотрите подраздел «Отбор признаков»). Существуют различные её разновидности, но основная идея в том, чтобы добавлять некоторую дополнительную информацию к условию с целью решить некорректно поставленную задачу или предотвратить переобучение. Эта информация часто имеет вид штрафа за сложность модели. Например, это могут быть ограничения гладкости результирующей функции или ограничения по норме векторного пространства (рисунок 2.12).

Рис. 2.12 – Пример регуляризации

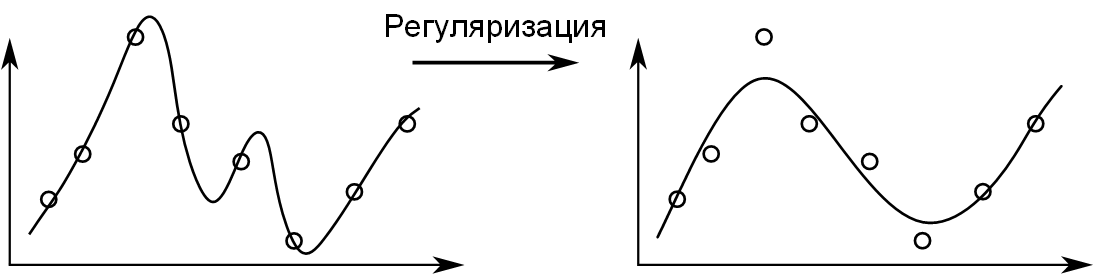
Если классификатор бинарный, т.е. имеет только два класса, тогда для оценки качества его работы можно применить таблицу неточностей (table of confusion):

Таблица неточностей 2.2 фактически отображает рисунок 2.8 в виде матрицы размером 2×2. Значения, которые расположены на диагонали матрицы, являются правильными ответами модели. Все недиагональные значения – это неправильные ответы.

Если количество классов классификатора больше двух, тогда метрикой качества классификации может быть матрица неточностей (confusion matrix), также известная как матрица ошибок (error matrix), которая представляет собой таблицу визуализации производительности алгоритма классификации при обучении с учителем. При обучении без учителя эту матрицу обычно называют матрицей соответствия (matching matrix). В таблице 2.3 показаны результаты классификации по трём классам.

Каждая строка матрицы неточностей представляет экземпляры в прогнозируемом классе, т.е. результат работы классификатора, в то время как каждый столбец представляет экземпляры в реальном классе, т.е. реальность либо некую экспертную оценку. Диагональные элементы матрицы неточностей являются правильными ответами классификатора. Все недиагональные элементы матрицы неточностей – это ошибки классификатора. Так классификатор выдал ответ, что обнаружено восемь картинок котов (сумма значений первой строки матрицы), однако в реальности из восьми картинок только пять являются правильными ответами, две картинки являются собаками и одна картинка – это кролик. Всего имеются девять изображений котов (сумма значений первого столбца матрицы). Три из этих девяти картинок были ложно классифицированы, как собаки, и одно изображение кота было ложно классифицирована, как кролик.

Матрицу неточностей для каждого конкретного класса можно преобразовать в таблицу неточностей для бинарного классификатора, например, таблица 2.4.

У бинарного классификатора часто есть порог, который можно регулировать, чтобы изменять ошибки первого (FP) и второго (FN) рода (рисунок 2.13).

Рисунок 2.13 – Порог бинарного классификатора может меняться

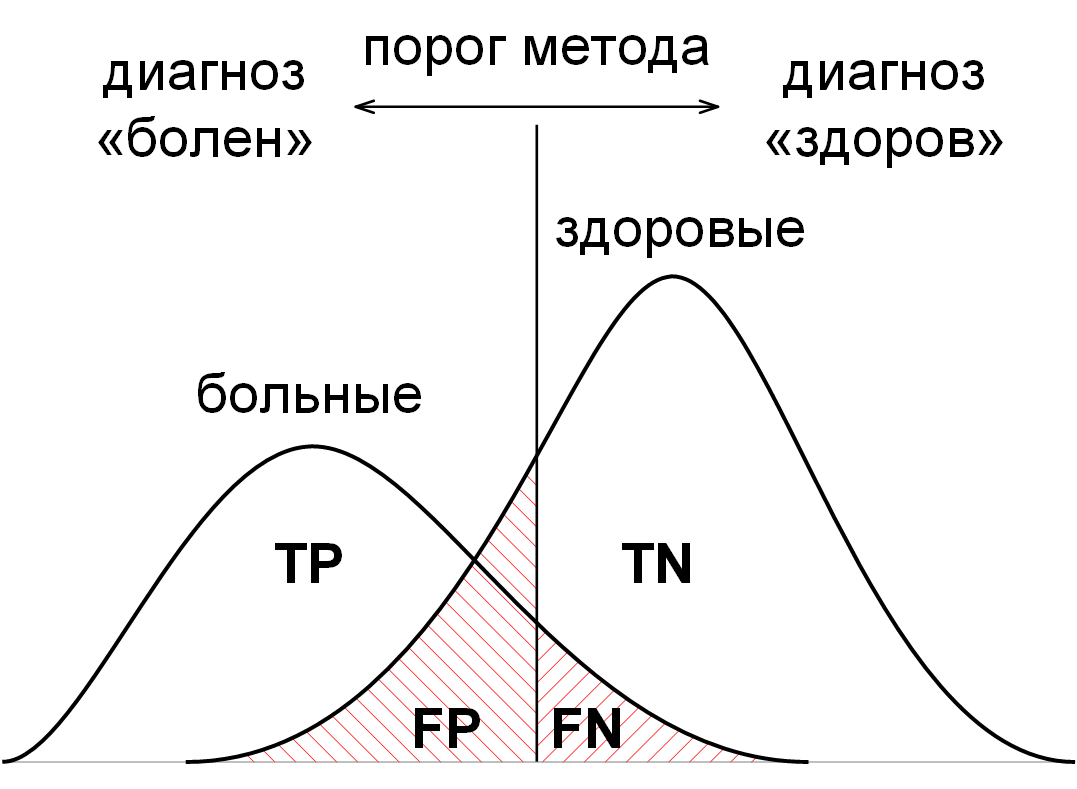
Если порог метода на рисунке 2.13 сдвинуть вправо, тогда метод будет правильно определять больше больных, но одновременно с этим в категорию больных будет попадать больше здоровых людей: ошибка первого рода увеличивается (FP), ошибка второго рода уменьшается (FN). Если порог метода сдвинуть влево, тогда метод будет правильно определять больше здоровых, но в категорию здоровых будет попадать больше больных людей: ошибка первого рода уменьшается (FP), ошибка второго рода увеличивается (FN).

Где выставить порог, чтобы получить оптимальный результат? Всё зависит от цены ошибки, которая различна для разных задач. Если важно найти всех больных, то можно пренебречь небольшим количеством ложных диагнозов для здоровых людей. Вместе с тем большое количество ложных срабатываний спам-фильтра может привести к потере важных писем.

По матрице неточностей, особенно для большого количества классов, трудно оценить модель в целом. Оценить модель в целом желательно одним числом. Одним из способов оценить модель в целом является AUC-ROC (или ROC AUC) – площадь (area under curve, AUC) под кривой ошибок (receiver operating characteristic curve, ROC-curve). Данная кривая представляет из себя линию от (0,0) до (1,1) в координатах True Positive Rate (TPR) и False Positive Rate (FPR) и является зависимостью верно классифицированных положительных примеров от неверно классифицированных отрицательных примеров (рисунок 2.14).

Рис. 2.14 – AUC-ROC-кривая и колоколообразные кривые для
плохого, хорошего и отличного методов классификации

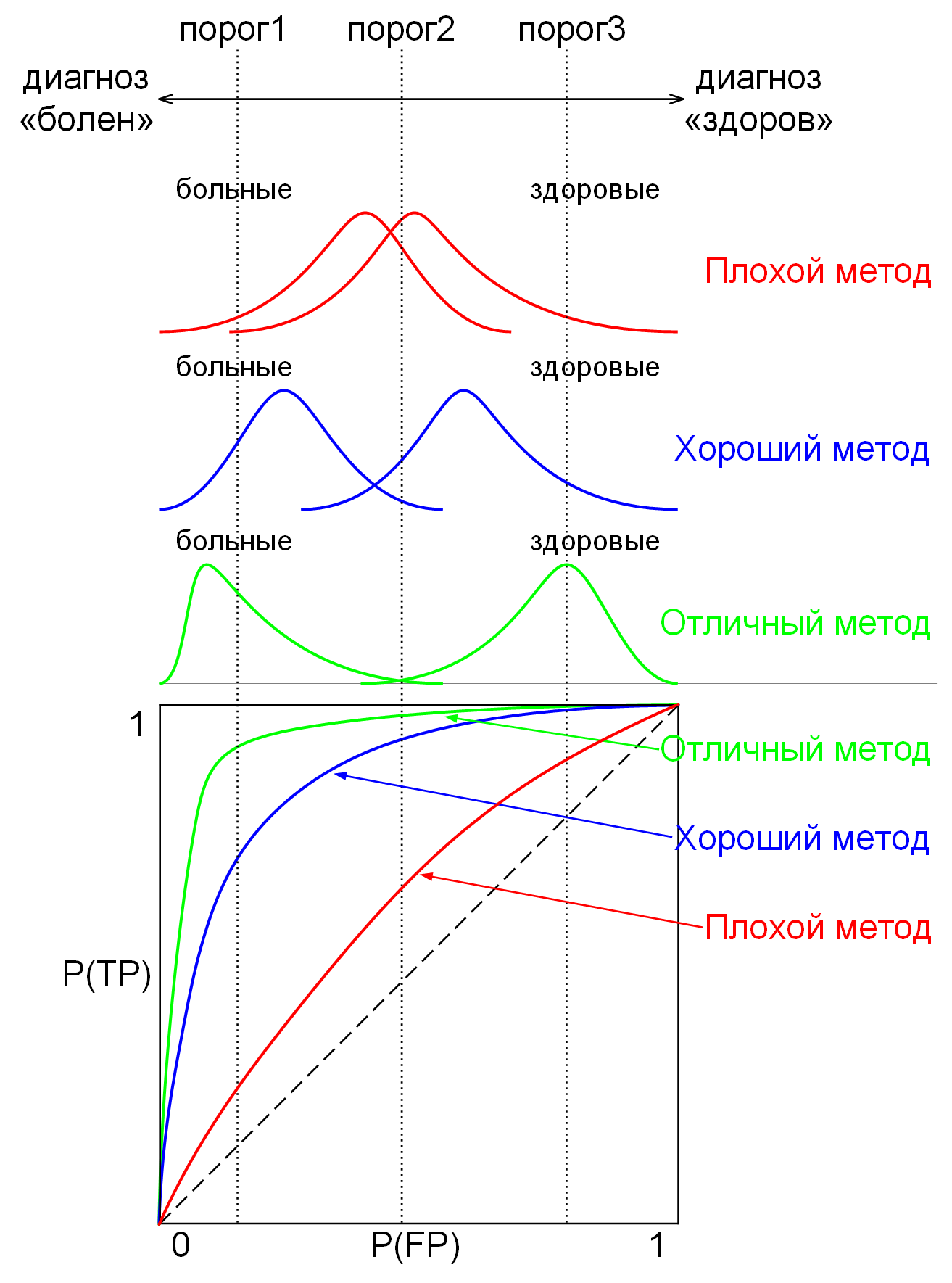
Качество разных методов можно сравнивать по площади под кривой ошибок (ROC AUC). Если площадь равна 0,5 (площадь прямоугольного треугольника), тогда метод является бесполезным, потому что его прогнозы ничем не отличаются от случайного угадывания или подбрасывания монеты. Площадь, равная 1,0 – это площадь идеального метода, который никогда не выдаёт ошибочных прогнозов. Качество реальных методов лежит в пределах отрезка [0,5; 1,0).

Оценка качества обучения зависит от выбранной метрики. Методы машинного обучения разделяются по типам решаемых задач. Каждый тип решаемых задач имеет свои собственные уникальные метрики: метрики качества кластеризации, метрики качества классификации, метрики качества ранжирования, метрики качества регрессии и т.д.

Так, например, метриками качества кластеризации являются похожесть и расстояние, которые выбираются в зависимости от условий задачи. Похожесть обычно обратная мера к расстоянию. Средняя похожесть в кластере выше, чем похожесть между элементами разных кластеров. Среднее расстояние в кластере меньше, чем расстояние между элементами разных кластеров. Метрики качества ранжирования (Mean Reciprocal Rank, Normalized Discounted Cumulative Gain, Precision@K, Recall@K и др.) необходимы для решения задач ранжирования и рекомендаций. Для метрик ранжирования важно учитывать порядок объектов и их позицию в списке.

После оценки качества обучения гиперпараметры ИНС изменяются и процесс обучения повторяется до достижения удовлетворительного результата.

Процесс решения задачи в машинном обучении

Процесс решения задачи в машинном обучении можно условно разделить на несколько шагов.

1. Изучить задачу, понять, как она может быть сведена к одной из типовых задач машинного обучения. Например, машинное обучение → обучение с подкреплением → управление роботом (рисунок 2.15).
   

Рис. 2.15 – Некоторые типовые задачи машинного обучения

2. Определить метод решения задачи средствами машинного обучения.
3. Получить данные для обучения. Аугментировать данные.
4. Отобрать, извлечь, спроектировать, преобразовать признаки.
5. Провести обучение модели.
6. Оценить результат с помощью различных метрик (в зависимости от задачи).
7. Повторить шаги 1–6 для других методов и параметров.

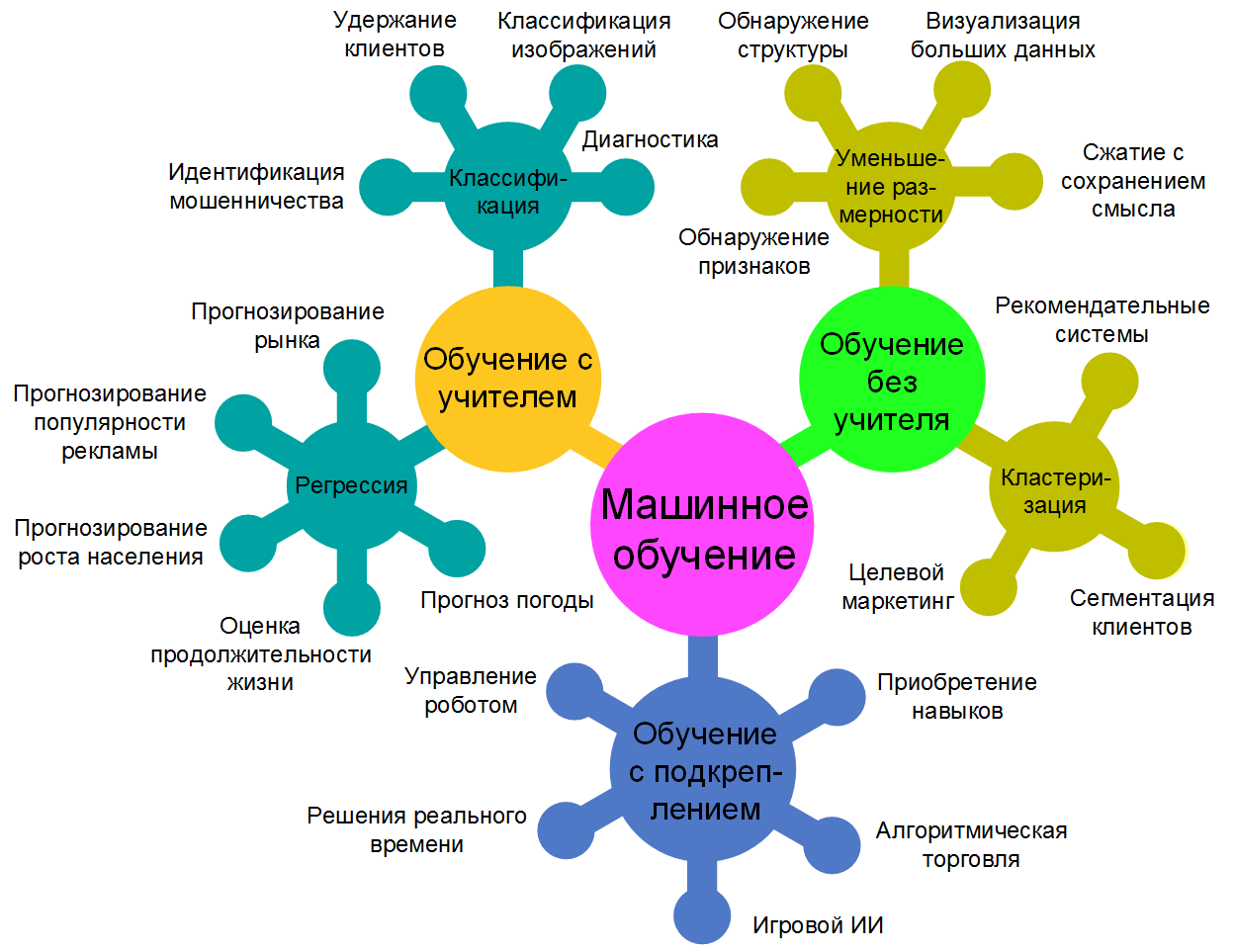
Существуют общие рекомендации для обучения ИНС [2.14, 2.15, 2.16, 2.17]. Кратко перечислим некоторые из них.

Машинное обучение – это не волшебство, оно не даёт что-то из ничего, но даёт большее из меньшего. В этом смысле машинное обучение похоже на сельское хозяйство. Как фермер комбинирует семена с питательными веществами, чтобы вырастить урожай, так знания комбинируются с данными, а дальше Природа делает за нас основную часть работы.

Прежде, чем обучать машину, разберитесь в задаче сами. Способ решения задачи неотделим от данных, которые используются в задаче: «No free lunch theorems».

Сбалансируйте ваши данные, подготовьте их, сделайте данные ценными: «Мусор на входе – мусор на выходе».

Больше данных лучше, чем более «умный» алгоритм.

Выбросы могут исказить метрику. Фильтруйте их или используйте регуляризацию.

Старайтесь использовать одну и ту же метрику для обучения и оценки качества.

Учитывайте цену ошибки, когда выставляете порог чувствительности метода.

Используйте тестовые данные только для проверки и не используйте их в обучении.

Если на обучающих данных точность ≈ 99%, а на тестовых данных точность ≈ 50%, то это переобучение.

Корреляция не доказывает причинную связь («Correlation is no proof of causation!»). Если есть корреляция между утонувшими в бассейне и фильмами с участием Николаса Кейджа, то этот факт не является поводом для обвинения актёра. Зачем же тогда искать корреляции? Прогнозные модели используются в качестве руководства к действию, для дальнейшего изучения. Если мы обнаружим, что пиво и подгузники в супермаркете часто покупаются вместе, возможно, стоит поместить пиво рядом с секцией подгузников для увеличения продаж.

Экспериментируйте. Комбинация методов лучше, чем выбор одного лучшего метода. Пробуйте разные методы обучения и способы получения признаков, а особенно их комбинации. Нет универсального метода для всех задач («There's no silver bullet»). Здесь интуиция и творчество так же важны, как и технические навыки, но само машинное обучение – контринтуитивная дисциплина.

Машинное обучение – это междисциплинарная наука, которая требует от исследователя широких знаний во многих дисциплинах.

Машинное обучение молодая и активно развивающаяся дисциплина, поэтому многие материалы есть только на английском языке.

Список литературы

2.1. Krizhevsky A., Sutskever I., Hinton G., ″ImageNet Classification with Deep Convolutional Neural Networks,″ NIPS'12 Proceedings of the 25th International Conference on Neural Information Processing Systems, Vol. 1, 2012, pp. 1097–1105.

2.2. Lecun Y., Bottou L., Bengio Y., Haffner P., ″Gradient-based learning applied to document recognition,″ Proceedings of the IEEE, Vol. 86, No. 11, Nov. 1998, pp. 2278–2324, doi: 10.1109/5.726791

2.3. He K., Gkioxari G., Dollár P., Girshick R., ″Mask R-CNN,″ IEEE International Conference on Computer Vision (ICCV), 2017, pp. 2980–2988, arXiv:1703.06870, doi: 10.1109/ICCV.2017.322

2.4. Zeiler M., Krishnan D., Taylor G., Fergus R., ″Deconvolutional networks,″ IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Jun. 2010, pp. 2528–2535, doi: 10.1109/CVPR.2010.5539957

2.5. Goodfellow I., et al., ″Generative adversarial nets,″ NIPS'14 Proceedings of the 27th International Conference on Neural Information Processing Systems, Vol. 2, 2014, pp. 2672–2680.

2.6. Elman J., ″Finding structure in time,″ Cognitive Science, Vol. 14, No. 2., 1990, pp. 179–211, doi: 10.1016/0364-0213(90)90002-E

2.7. Jozefowicz R., Zaremba W., Sutskever I., ″An Empirical Exploration of Recurrent Network Architectures,″ ICML'15 Proceedings of the 32nd International Conference on Machine Learning, Vol. 37, Jul. 2015, pp. 2342–2350.

2.8. Greff K., Srivastava K., Koutník J., Steunebrink R., Schmidhuber J., ″LSTM: A search space odyssey,″ IEEE Transactions on Neural Networks and Learning Systems, Vol. 28, No. 10, Oct. 2017, pp. 2222–2232, doi: 10.1109/TNNLS.2016.2582924

2.9. He K., Zhang X., Ren S., Sun J., ″Deep residual learning for image recognition,″ IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, 2016, pp. 770–778, doi: 10.1109/CVPR.2016.90

2.10. Kulkarni T., Whitney W., Kohli P., Tenenbaum J., ″Deep convolutional inverse graphics network,″ NIPS'15 Proceedings of the 28th International Conference on Neural Information Processing Systems, Vol. 2, 2015, pp. 2539–2547.

2.11. Simonyan K., Zisserman A., ″Very Deep Convolutional Networks for Large-Scale Image Recognition,″ arXiv preprint, 2014. arXiv:1409.1556

2.12. Lee H., Grosse R., Ranganath R., Ng A., ″Convolutional Deep Belief Networks for Scalable Unsupervised Learning of Hierarchical Representations,″ ICML '09 Proceedings of the 26th Annual International Conference on Machine Learning, 2009, pp. 609–616, ISBN: 978-1-60558-516-1, doi: 10.1145/1553374.1553453

2.13. LeCun Y., Bottou L., Orr G., Müller K., ″Efficient BackProp″, ″Neural Networks: Tricks of the Trade″, chapter 2, Springer-Verlag Berlin Heidelberg, 1998, pp. 9–50, ISBN: 3-540-65311-2

2.14. Domingos P., ″A Few Useful Things to Know about Machine Learning,″ Communications of the ACM, Vol. 55, No. 10, Oct. 2012, pp. 78–87, doi: 10.1145/2347736.2347755

2.15. Domingos P., ″The Master Algorithm: How the Quest for the Ultimate Learning Machine Will Remake Our World,″ Basic Books, New York, NY, 2015, p. 352. ISBN: 978-0465065707

2.16. Bostrom N., ″Superintelligence: Paths, Dangers, Strategies,″ Oxford University Press, 2014, p. 328. ISBN: 978-0199678112

2.17. Herbert A. Simon, ″Spurious Correlation: A Causal Interpretation,″ Journal of the American Statistical Association, Vol. 49, No. 267, Sep., 1954, pp. 467–479, doi: 10.1080/01621459.1954.10483515